New ENSO Forecasts Based on Solar Model

by   Dr Theodor Landscheidt  (22 Dec 2003)

Schroeter Institute for Research in Cycles of Solar Activity
Klammerfelsweg 5, 93449 Waldmuenchen,Germany
th.landscheidt@t.online.de

1. Introduction

Anomalous warming (El Niño) or cooling (La Niña) of surface water in the eastern equatorial Pacific occurs at irregular intervals (2 to 7 years) in conjunction with the Southern Oscillation (SO), a massive seesawing of atmospheric pressure between the south-eastern and the western tropical Pacific. The coordinated El Niño/Southern Oscillation phenomenon (ENSO), also including La Niña, is the strongest source of natural variability in the global climate system. Anomalies in the global temperature (positive or negative deviations from a defined mean temperature) are primarily driven by ENSO events (Peixoto and Oort, 1992).

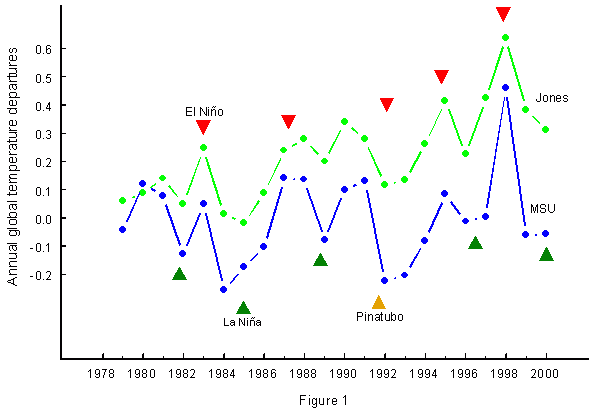
Figure 1 shows this clearly. The green curve presents global temperature anomalies based on surface observations (Jones) while the blue curve is based on satellite data (MSU). Though the amplitudes of the two curves are quite different, they reach peaks and troughs at nearly the same time. Red triangles mark El Niño events and green triangles La Niña episodes.  El Niños consistently coincide with peaks in global temperature and La Niñas with troughs. There is only one exception around the Pinatubo eruption indicated by a yellow triangle. When explosive volcanic activity intervenes, global temperature is modulated by its cooling effect.

The importance of ENSO activity for global climate has recently been corroborated by an investigation which shows that the variability of the Pacific Decadal Oscillation (PDO) is subjected to direct forcing by El Niños and La Niñas, not vice versa, so that predicting the PDO may be directly related to the skill of forecasting ENSO (Newman et al., 2003).

So it is plausible that there are strong links between ENSO events and the seasonal course of weather in other world regions. As this might be the key to long-range seasonal forecasts, there is strong interest in precursors that could make it possible to predict ENSO events. Daily observations of changes in sea surface temperature (SST), surface wind, upper ocean thermal structure, and ocean currents enable researchers to develop models that can be tested by experimental forecasts. It seems to be very difficult, however, to design models that extend the limit of several months set by the observation of precursors. Zane and Zebiak of the Lamont-Doherty Earth Observatory made the first successful forecast of an El Niño in early 1986, one year ahead of the event, but their model did not predict the strong El Niño in 1997. 

At present, there exist no physical or statistical models that can skilfully predict ENSO events at lead times longer than 12 months (Neelin and Latif, 1998). Landsea and Knaff (2000), who employed a statistical tool to evaluate the skill of twelve state-of–the-art climate models in real time predictions of the development of the 1997-1998 El Niño, have shown that the models exhibited essentially no skill in forecasting the event at lead times ranging from zero to eight months.

According to Neelin and Latif (1998) weather noise and deterministic chaos, representing the internal variability of the climate system, set the fundamental limits to the lead time. This emphasis on the exclusively internal character of ENSO events is in accordance with the tenet of climatology that ENSO phenomena are the most spectacular example of a free internal oscillation of the climate system not subjected to external forcing (Peixoto and Oort, 1992). It has been shown that this tenet is not tenable because there is external forcing exerted by solar activity to such a degree that long-range ENSO forecasts can be based on it.  I correctly predicted the last three El Niños, years before the respective events, and also the course of the last La Niña (Landscheidt, 2002), though the forecast was exclusively based on the Sun’s variable eruptive activity.  (See special note by John L. Daly re. this claim).  Meanwhile, I have been working on this solar model to improve it.  The advanced version is presented here together with new detailed ENSO forecasts. 



2. Maximum of solar eruptions in the 11-year sunspot cycle

The sunspot maximum of the 11-year cycle is a well known feature.  In the literature, the length of the sunspot cycle is not only measured from minimum to minimum, but also from maximum to maximum.  Yet it is scarcely known that there is also a maximum of the Sun’s eruptional activity (flares, coronal mass ejections, and eruptive prominences) within the 11-year cycle.  It is shown here that it can be defined in a precise way. Consecutive maxima of eruptions (EM) form cycles of their own - from EM to EM - which also have a mean length of 11 years.  They are of special import as they are closely linked to ENSO activity.

The 11-year sunspot cycle is not symmetric.  Reliable observations available since 1750 show that the mean rise to the sunspot maximum (4.3 years) is considerably steeper than the decline to the sunspot minimum (6.7 years).  In the mean cycle normalized to 1, the ratio of the rising part to the whole cycle is 0.39 and of the descending part to the complete cycle 0.61.  This is close to the proportion of the golden section which divides a frame structure like a line segment, a surface, a cycle, or any other delimited feature so that the ratio of the smaller part (minor) to the larger part (major) equals the ratio of the larger part to the whole. When the whole is set equal to 1, we get

0.3819 … : 0.618 … = 0.618 … : 1. 

To find the approximate major of the length of a cycle, it has to be multiplied by 0.618. Multiplication by 0.382 yields the minor. This makes it easy to see that according to observations going back to 1750 the sunspot maximum falls nearly exactly at the minor of the golden section when the cycle is measured from minimum to minimum.

This is not merely a queer coincidence. It is well known that the golden section has not only astounding mathematical qualities, but also orchestrates the growth of plants and regulates neuron stability (Kappraff, 1991).  Yet even scientists are often not aware of physical functions of the golden section, especially in celestial dynamics.  There is mathematical proof that the golden number G = 0.618 … is the most irrational number in all classes of numbers.  This quality links it to the stability of the solar system as the mathematicians and physicists Siegel (1942), Kolmogorov (1979), Arnol’d (1963) and Moser (1973) have shown.  This is crucial, as a 100-million year integration of the solar system (Sussman and Wisdom (1992) provides evidence that all planetary orbits are chaotic with a time scale for exponential divergence of about 4 million years.  In my paper “The Cosmic Function of the Golden Section" (Landscheidt, 1995) I have shown how the golden section as a stability parameter has kept the solar system stable for 4.6 billion years in spite of chaos in all planetary orbits.  The stabilizing function of the golden section is not confined to macroscopic dynamical systems.  Child (1993) and Mackay, Meiss and Percival (1987) have provided evidence that it governs the inner dynamics of molecules at energies approaching the ionization threshold.  The fact that the ascending part of the 11-year sunspot cycle equals the minor and the descending part the major of the golden section contributes to the stabilization of solar activity which is characterized by phenomena generated by instability.

In this light, it makes sense that first investigations indicate that the maximum of eruptions EM falls at 0.618 of the unit cycle.  It establishes symmetry within the 11-year cycle as sunspot maximum (SM) and EM at 0.382 and 0.618 show bilateral symmetry with respect to 0.5 at the middle of the cycle. The interval from EP to EP turns out to be a cycle (EMC) which as well as its second harmonic (EMC/2) is closely connected with ENSO events.

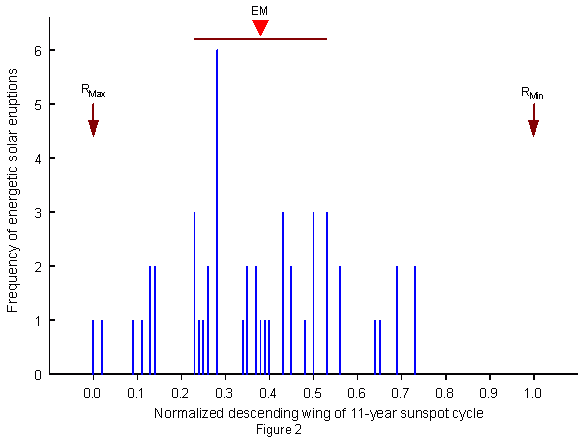
Figure 2 presents a first assessment of the position of EM checking the working hypothesis that EM falls at 0.618 of the unit cycle. It shows the frequency distribution of energetic solar eruptions within the descending part of the 11-year sunspot cycle from maximum to minimum as indicated by arrows.  The sample covers all energetic flares X => 6 observed by satellites from 1970 to present.  These data are available at the National Geophysical Data Center, Boulder.  Intense X-ray flares, nearly always accompanied by heavy coronal mass ejections, are geophysically more effective than flares categorized into classes of optical brightness.  Before 1970, there were no continuous satellite observations of X-ray flares.  This is why all highly energetic cosmic ray flares observed between 1942 and 1970 were included as listed by Sakurai (1974) and Smith and Smith (1963). The total sample comprises 49 extremely energetic eruptions. The descending wings of the sunspot cycles between 1942 and present were normalized to have equal unit length to make it easy to recognize identical phases of events in different cycles.

The hypothetical position of EM at 0.618 of the 11-year cycle normalized to 1 is marked in Figure 2 by a red triangle.  A range of  ±0.15 around EM is indicated by a horizontal bar.  As expected, the energetic eruptions accumulate in this region close to EM.  As many as 33 of the 49 eruptions fall at this range. The recent spectacular eruptions covered by media reports, too, are to be found in this region.  Close to the sunspot maximum RMax, however, only a few eruptions were observed. 

In a statistical evaluation based on traditional expectations it would have seemed reasonable to assume a maximum of eruptions around RMax and a descending frequency parallel to the course of the diminishing sunspot activity.  This expected frequency, however, would be exposed to objections.  As can be seen from Figure 2, beyond 0.75 of the scale there are no longer any strong eruptions observed as this is too close to the minimum of the cycle.  Moreover, it seems more objective to expect an equal distribution in the whole area covered by eruptions from 0 to .75 on the scale so that any predilections are avoided.  A Pearson-test on this basis with two classes, one ±0.15 around EM and the other one comprising the rest of the scale up to 0.75, yields Chi² = 15.3 for 1 degree of freedom and P < 0.0001. Re-sampling confirms this result.  As EM falls just at the center of the most frequent eruptions, the hypothesis that the mean position of EM is identical with the major of the golden section at 0.618 of the scale cannot be rejected.

This is corroborated by an additional result.  As Figure 2 shows only the frequency distribution in the descending wing of the cycle normalized to 1, the position 0.618 in the whole cycle is identical with 0.382 on the scale in Figure 2.  The weighted mean of the observed frequency distribution in Figure 2 is equal to 0.37.  This is rather close to the hypothetical position of EM at 0.382. 

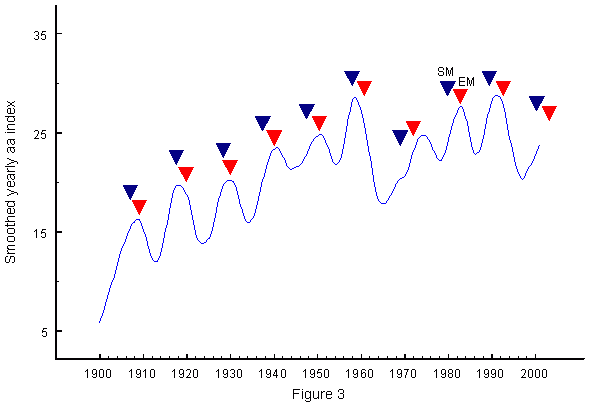
The investigation of energetic eruptions covers only the sunspot cycles from 1970 on.  Figure 3 extends the assessment of EM back to 1900.  The geomagnetic aa index (Solar-Geophysical-Data, 2003) measures the effect of solar eruptions near Earth.  The blue curve in Figure 3 shows the smoothed aa index from 1900 to 2000.  Hypothetical EM positions at 0.618 are marked by red triangles and the sunspot maxima (SM) by blue triangles.  It can clearly be seen that the position of EM nearly always coincides with the aa maxima indicating phases of strong eruptional activity on the sun.  There are only two exceptions: the aa maxima around 1958 and 1990 occurring within exceptionally short and intense sunspot cycles.  In such cases the aa maximum seems to develop earlier than hypothesized.  Obviously, the SM is a bad indicator of the most eruptive phase in the sunspot cycle.

3. El Niño and La Niña linked to cycles based on EM and SM

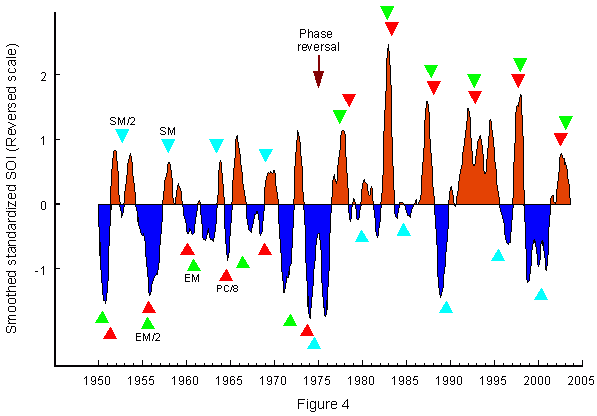
The curve in Figure 4 shows slightly smoothed standardized monthly data of the SOI, the Southern Oscillation Index (Climate Prediction Center, 1998).  It measures the pressure gradient across the tropical Pacific which, in turn, is an indicator of equatorial wind variations.  Low negative SOI values, indicating El Niños, go along with weaker than normal trade winds over the central Pacific, warmer than normal sea surface temperatures (SST) over the eastern equatorial Pacific, and a reduced westward pressure gradient with changing wind stress values.  High positive SOI values indicate La Niña conditions, just the opposite of the El Niño scenario.  In Fig. 4 the data are reversed so that strong positive peaks point to El Niños (red areas) and negative deviations to La Niñas (blue areas). 

It is evident that the cycle running from EM to EM (EMC) and its second harmonic are closely connected with ENSO events.  EM and the zero phase of its second harmonic (EM/2) are indicated by green triangles.  Before the phase reversal, indicated by an arrow, the EM and EM/2 phases coincide with La Niñas and afterwards with El Niños.  The sunspot maximum SM as well as the second harmonic of a cycle running from SM to SM (SMC) show a similar connection, though reversed.  SM and the zero phases of the second harmonic (SM/2) are marked by triangles in cyan colour.  Before the phase reversal SM and SM/2 go along with El Niños and afterwards with La Niñas.  The effects of EMC and SMC seem to be of opposed polarity, but the pattern before and after the phase reversal overall shows balanced symmetry, similar to EM and SM with respect to 0.5 in the 11-year unit cycle. 

4. Phase reversals in solar cycles connected with ENSO events

In nearly all of my papers I could show that there are phase reversals in the climate time series related to solar cycles.  These are not ad hoc inventions, but computable phases of instability that usually occur when zero phases of longer solar motion cycles coincide with zero phases of shorter solar motion cycles.  Without such knowledge forecasts would lead astray.  A predicted El Niño could turn out to be La Niña, or vice versa.  Thorough analysis has disclosed that with regard to ENSO events there is another pattern of phase reversal that had escaped my notice. 

I have shown that the North Atlantic Oscillation (NAO), the Pacific Decadal Oscillation (PDO), extrema in global temperature anomalies, drought in Africa and U.S.A., as well as European rainfall and floods are linked to cycles in the sun’s irregular orbital motion around the center of mass of the solar system (Landscheidt, 1983-2003).  The rate of change of the sun’s orbital angular momentum L - the rotary force dL/dt driving the sun’s orbital motion (torque) - forms a torque cycle (TC) with a mean length of 16 years (Landscheidt, 2001a,b).  Perturbations in the sinusoidal course of this cycle recur at quasi-periodical intervals and mark initial phases of a perturbation cycle (PC) with a mean length of 35.8 years.  As to details, I refer to Figure 2 of my on-line paper “Solar eruptions linked to North Atlantic Oscillation” (Landscheidt, 2001 a). 

The zero phases of the PC play an important role in the long-range forecast of diverse climate phenomena.  They indicate, for instance, the peaks of warm PDO regimes, the coolest phases of cold regimes, and shifts between these regimes (Landscheidt, 2001b) They are also linked to extended dry and wet spells measured by the U.S. drought index (Landscheidt, 2003a).  As to the details and physical implications of the Sun’s irregular orbital motion I refer to my papers “New Little Ice Age instead of global warming?” (Landscheidt, 2003b) and “Extrema in sunspot cycle linked to Sun’s motion" (Landscheidt, 1999).

Another approach to the 35.8-year cycle has been presented in Fig. 3 of my paper “Trends in Pacific Decadal Oscillation subjected to solar forcing” (Landscheidt, 2001b).  It has been shown that absolute values of the torque cycle (|dL/dt|) form a shorter cycle that plays, e. g., a major role in solar forcing of the North Atlantic Oscillation (Landscheidt, 2001a) and discharges in river catchment areas (Landscheidt, 2000c,d ).  When a Gaussian low-pass filter suppressing wavelengths shorter than 9 years is applied to |dL/dt|, new oscillations emerge as shown in Fig. 3 of the quoted paper for 1721 - 2077.   Minima in the smoothed |dL/dt|-curve are identical with initial phases in the 36-year perturbation cycle.  So it is easy to compute the precise dates of these phases for any period, as for instance 1829.5, 1867.2, 1901.8, 1933.6, 1968.9, 2007.2, 2044.9., and 2080.7.

Nature often repeats well-tried patterns on different scales.  When the 36-year cycle is considered to be part of a fractal that also comprises the 11-year sunspot cycle, to which it is linked by the Sun’s dynamics, the phase of the minor 0.382, comparable to the sunspot maximum in the 11-year cycle, may be expected to have special functions.  One of them is, as far as I can see, the induction of phase reversals in subordinated cycles.  Especially solar cycles that are linked to ENSO events are affected. This was confirmed by a comparison of Quinn’s El Niño index (Quinn et al., 1987) going back to 1525 with phases 0.382 in respective 36-year cycles.  This morphological relationship makes sense as the solar magnetic field reverses its polarity when the 11-year cycle reaches the sunspot maximum. 

The initial phase of the current PC falls at 1968.9 and this cycle ends in 2007.2.  So the minor 0.382 falls at 1983.5.  The actual phase reversal, however, occurred in 1976 as will be confirmed by additional data presented in Figures 4 and 5.  This is the only exception in more than 200 years.  Unfortunately, just in the present cycle important for the current forecast another factor intervened, namely the 179-year cycle in the Sun’s motion.  Jose (1965) has found patterns in the rate of change in the Sun’s orbital angular momentum that repeat at intervals of 178.8 years. In his pioneering computer analysis of the Sun’s motion he discovered that sunspots, too, follow a cycle of this length. 

According to Dansgaard et al. (1973), a period of 181 years, rather close to 179 years, is the paramount cyclic feature of the oxygen isotope profile of the Camp Century ice core. This indicates a connection with climate I dealt with in several papers (Landscheidt, 1983-2003).  The Jose cycle could be shifted arbitrarily.  I have shown, however, that it has well defined initial phases that fall, for instance at 1545.1, 1723.1, 1901.8. and 2080.7.  As to a plot of the 179-year cycle I refer to Figure 3 of my on-line paper “Trends in Pacific Decadal Oscillation subjected to solar forcing” (Landscheidt, 2001b). 

The 179-year cycle, also linked to the Sun’s dynamics, may be considered to be part of a comprehensive fractal that also comprises the 36-year cycle and the sunspot cycle so that the minor of the golden section also induces phase reversals in subordinated cycles.  In the current cycle running from 1901.8 to 2080.7 the minor 0.382 falls at 1970.1.  Detailed analysis shows that the phase reversal in 1976, indicated in Figures 4 and 5 by arrows, occurred just at the midpoint 1976.8 between 1970.1 and the 0.382 phase 1983.5 in the 36-year cycle.  As the 0.382 phase in the following 36-year cycle will not be reached before 2021, the pattern should continue as indicated in Figures 3 and 4 after the phase reversal in 1976.  Those who want to make forecasts themselves should understand that a solution of the problem of phase reversals, neglected or even ridiculed by most climatologists, is crucial to skilful forecasts of ENSO episodes and other climate phenomena regulated by solar activity.

Intriguingly, the phase reversal in 1976 went along with a crucial regime and trend shift in global temperature.  It is acknowledged that three phases can be distinguished in the development of global temperature:  Steep rising trend from a deep point around 1910 to a crest about 1945, a cooling trend from 1945 to 1976, and from then on again a rising trend.  The last regime shift in 1976 coincided with the described phase reversal in 1976.  The phase reversals indicated by the phases 0.382 in the two preceding PCs fall at 1947.1 and 1913.9.  They also coincide with the respective regime shifts.

5. Harmonics of perturbation cycle PC connected with ENSO episodes 

The red triangles in Figure 4 indicate zero phases of the 8th harmonics (PC/8) of the 36-year solar motion cycle described above. Up to the phase reversal in 1976, these PC phases coincide with La Niñas and after the phase reversal with El Niños.  It results in the same pattern of variations as with EM and EM/2.  It should be noted that this seems to explain the preponderance of La Niñas up to 1976 and of El Niños after the phase reversal.  Predominant La Niñas and El Niños are indicated by two factors from quite different solar cycles nearly simultaneously, whereas El Niños before 1976 and La Niñas after 1976 are only connected with a single solar factor.  This seems to have a quantitative effect. 

6. Special torque cycle involved in solar forcing of ENSO events

A further factor that seems to contribute to the solar triggering of El Niño and La Niña is a special form of the 16-year torque cycle TC described above. Its consecutive zero phases have a different quality. The Sun’s orbital motion, from which the cycle is derived, is governed by difference forces in the same way as the planets’ course around the Sun. Gravitation and centrifugal force are balanced overall, but in special phases of the orbit one of the two forces may prevail.  Zero phases Zg initiate a period of prevailing gravitation and an orbital motion towards the centre of mass (CM) of the solar system, whereas the respective neighbouring zero phases Zc mark the start of dominant centrifugal force and a motion away from the CM.  These changes in the physical quality of the solar motion have a strong effect on the distribution of solar eruptions in different regions of the Sun (Landscheidt, 1986 a).

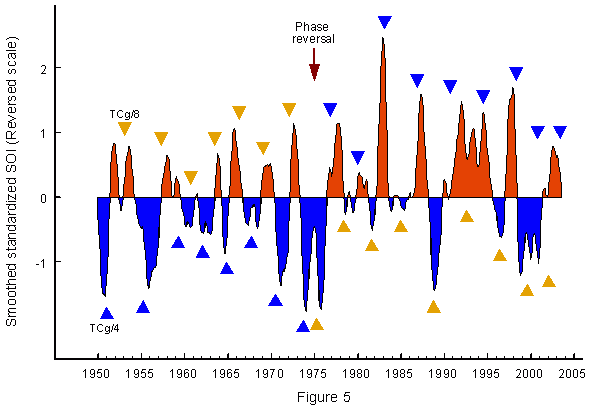
Torque cycles measured from Zg to Zg (TCg) have a mean length of 16 years, but there are strong variations between 10 and 23 years.  Figure 5 shows a close connection between TCg and ENSO events.  Zero phases of the 4th harmonic of TCg (TCg/4) are marked by blue triangles.  Before the phase reversal they consistently coincide with La Niñas and after 1976 with El Niños.  Zero phases of the 8th harmonic of TCg (TCg/8) are indicated by yellow triangles.  They have the opposite effect.  Before the phase reversal they are coeval with El Niños and after 1976 with La Niñas.  Again there is overall symmetry.  As to the preponderance of La Niñas up to 1976 and El Niños after 1976 there is no essential change.  Without inclusion of the results presented in Figure 5 the ratio of the forcing was 2 to 1 and with inclusion 3 to 2 in favour of the predominant phenomenon.  Again, the precision of the phase reversal is impressive,  especially as the TCg phases are derived from another quite different solar cycle.

A comparison of Figures 4 and 5 shows that of the five solar factors involved – EM and EM/2, SM and SM/2, PC/8, TCg/4, and TCg/8 - often two or three are related to a single ENSO episode.  The mean of their dates indicates the peak of the ENSO effect.  If in rare cases not all of the single events presented in one of the Figures 4 and 5 are covered by one of the factors, a proper link is to be found in the other figure.  If factors with opposite effect coincide, this cripples the ENSO response.  TCg/4 in 1980 and SM in1979.9 are a case in point. 

7. New Forecasts of El Niño and La Niña

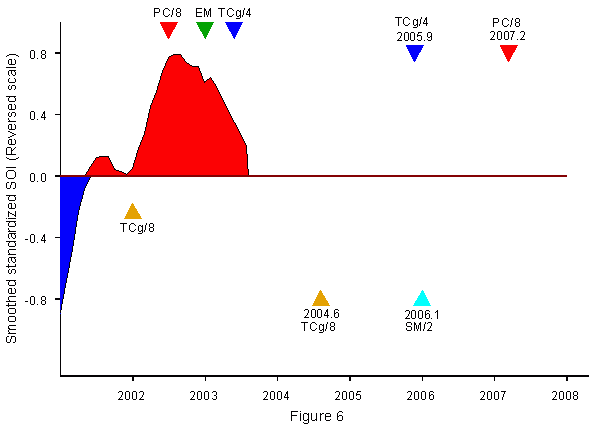
Figure 6 shows on the left the development of the last El Niño. The steep rise from the last cool episode to warm conditions, initiated by PC/8, was interrupted by TCg/8, but then supported by EM and TCg/4. As TCg4 fell at 2003.4, warm SST in the equatorial Pacific lingered far into 2003.  A La Niña episode could not develop. As there is no other factor around that could interfere, neutral conditions should prevail from December 2003 to at least April 2004 (Probability 85 %).

TCg/8 in 2004.7, favouring cool conditions, is expected to release La Niña after April 2004 and last at least till April 2005 (Probability 90 %).

The forecast for the rest of the year 2005 is more difficult than at other times, as can be seen when Figure 6 is compared with Figures 4 and 5.  TCg/4 in 2005.9 would release an El Niño lasting from about May 2005 to April 2006 if it were not opposed by SM/2 which is expected to occur at the beginning of 2006.  It is probable (75%) that conditions like around 1980 will develop when TCg/4 in 1980 and SM in 1979.9 released opposing potentials at the same time.  Figures 4 and 5 show that around 1980 there was only slight warming that did not reach the level of an El Niño.  These conditions should last at least till May 2006. This situation would change if the next 11-year sunspot cycle No. 24 would turn out to be so weak that it reached the unusual length of more than 12 years. SM/2 would then shift to a later date and no longer oppose TCg/4.

PC/8 in 2007.2 has El Niño potential. As the date 2007.2 is closer to 2006/2007 than to 2007/2008 it is to be expected that El Niño will already emerge around July 2006 and last at least till May 2007 (Probability 80 %). The alternative to this early date is a release of the expected El Niño around April 2007; it should last till January 2008 (Probability 20 %).

As to a definition of ENSO based on the Southern Oscillation Index I refer to my paper “El Niño forecast revisited” (Landscheidt, 2002). This definition is in accord with the NOAA’s declarations about the state of ENSO published by the Climate Prediction Center/NCEP

8. Physical background and outlook

In spite of my well-documented successful ENSO forecasts years ahead of the respective events it is to be expected that the presented results will be dismissed as a statistical artefact as there is no detailed causal explanation in strict terms of physics.  This is no valid argument, however, as long as climatologists do not know how El Niño and La Niña come into existence.  It is only known which meteorological processes go along with the development of ENSO episodes, not what releases them. So critics nonsensically demand a physical explanation of the solar relationship to processes that have not yet been explained by climatologists.

Though there are no strict physical arguments that could explain in detail how solar activity causes ENSO events, it is possible to develop working hypotheses that suggest potential mechanisms that could be of import if climatologists find out how El Niño and La Niña are triggered.  Flares increase the Sun's UV radiation by at least 16%.  Ozone in the stratosphere absorbs this excess energy which causes local warming and displaces the 70-mb polar vortex.  This disturbance in the circulation is propagated downwards to the troposphere where it affects the intensity of the Hadley circulation.  Hartley et al. (1998) have shown that there is a dynamical link between stratospheric polar vortex distortions and meteorological events in the troposphere.

General circulation models developed by Haigh (1996), Shindell et al. (1999), and Balachandran et al.(1999) confirm that circulation changes initially induced in the stratosphere can penetrate into the troposphere and influence temperature, air pressure, Hadley circulations and storm tracks by changing the distribution of large amounts of energy already present.  As ENSO events are linked to trade winds and trade winds to Hadley cells that may be affected by flare induced circulation change in the stratosphere, it seems plausible that energetic solar eruptions may be an essential link in the causal chain triggering ENSO events, especially if there is a barrage of solar eruptions covering weeks.

Solar X-rays around 10 Å intensify by a factor of 100 or more during moderate-sized flares while strong flares can amplify the X-ray level by a factor of 1000.  I refer to my paper “Solar rotation, impulses of the torque in the Sun’s motion, and climatic variation” (Landscheidt, 1988) which describes how X-rays produced by energetic solar eruptions may enhance thunderstorm activity.  Severe thunderstorms are linked to tropical cyclones (Williams, 1977) which may trigger and sustain El Niños (Ramage, 1986).

Another possibility are seismic predictors of El Niño connected with solar eruptions.  El Niños occur during sustained simultaneous abnormal weakenings of the high pressure cell in the South Pacific generally centered near Easter Island and abnormal strengthening of the low pressure cell near northern Australia.  Walker (1995,1999) has found that located on the seafloor within the same region is one of the Earth’s most rapidly spreading mid-ocean ridge system affected by strong seismic activity just before El Niños begin to develop.  As the correlation between the seismic predictor and El Niños is highly significant, Walker assumes that massive episodic thermal intrusions may play an important role in disrupting the east-to-west interactions of the high and low pressure cells.  Handler (1989) and recently Adams et al. (2003) also assume a connection between seismic activity and El Niños, but base them on explosive tropical volcanic forcing via aerosols.

According to Walker (1999) the rapidly spreading ridge system includes the Easter and Juan Fernandez microplates.  Accumulated strain between such plates can be released by jumps in the Earth’s rotational velocity.  Rotational jumps of this kind were observed after energetic solar flares (Danjon, 1959, 1960). The length of day increases in such cases by two milliseconds and it takes half a year to regain the rotational state before the flare.  Strong geomagnetic activity reflects strong flare activity and could be indicative of jumps in the Earth’s rotation.  When I compared the geomagnetic aa index with seismic activity, I found a highly significant correlation.  The result will be published in a separate paper.

There can be no doubt that solar eruptions generally have a strong effect on weather and climate as its integral.  There are hundreds of observations which show clearly that within a few days after solar flares, coronal mass ejections, or eruptive prominences there are diverse meteorological responses of considerable strength.  As to the wealth of publications I refer to Chapter 4 of my paper “Long-range forecast of U.S. drought based on solar activity” where I also quote papers on physical models that could explain the effect of solar eruptions on climate. 

Even if there were no such observations and potential physical models, the lack of a viable mechanism is not a valid scientific argument as most studies in natural sciences begin without knowledge of the responsible mechanisms (Roederer,1993). Many practices in meteorology are on this heuristic level and mankind made use of electricity long before anyone knew that there are electrons.  Epistemologically, the stages of gathering data, establishing morphological relationships, and setting up working hypotheses necessarily precede the stage of elaborated theories.  We are able already to discern underlying patterns in a seemingly impenetrable thicket of data without correlations.  Predictability, based on such patterns is one of the corner stones of science.  Open-minded scientists should cooperate to achieve progress in this field.

IPCC proponents prayer-wheel-wise repeat the mantra that in recent decades the effect of solar activity, still prevalent in the first half of the 20th century, has marvellously disappeared.  My correct long-range forecasts of the last three El Niños and the course of the last La Niña, exclusively based on solar activity, and the additional results presented in Figures 4 and 5 of this paper are evidence to the contrary.

Acknowledgement:

I confirm that I did this work without any support from any side. 

References:

Adams, J. B., Mann, M. A., and Ammann, C. M. (2003): Proxy evidence for an El Niño-like response to volcanic forcing. Nature 426, 274-278.

Arnol’d, V. I. (1963): Small denominators and problems of stability in classical and celestial mechanics. Russ. Math. Surv. 18,85.

Balachandran, N. K., Rind, D., and Shindell, D. T., 1999: Effects of solar cycle variability on the lower stratosphere. J. Geophys. Res. 104, 27321-27339.

Child, M. S. (1993): Nonlinearity and chaos in atoms and molecules. In: Mullin, T., ed.: The nature of chaos. Oxford, Clarendon Press, 272.

Climate Prediction Center (1998): NOAA, Data and Indices. < http://nic.fb4.noaa.gov >

Danjon, A. (1959, 1960): Solar flares and changes in the length of day. C. R. Acad. Sci Ser. B; 249 (1959); 250 (1969).

Dansgaard, W., Johnsen, S. J., Clausen, H. B., and Langway, CC. (1973): Climatic record revealed by the Camp Century ice core. In: Turekian, K. K., ed.: The late Cenocoic ice ages. New Haven, Yale University Press, 43-44.

Haigh, J. D.,1996: On the impact of solar variability on climate. Nature 272, 981-984.

Handler, P. (1989): The effect of volcanic aerosols on global climate. J. Volcan. Geoth. Res. 37, 233-249.

Hartley, D. E., Villarin, J. T., Black, R. X., and Davis, C. A. (1998): A new perspective on the dynamical link between the stratosphere and the troposphere. Nature 391, 471-474.

Jose, P. D. (1965): Sun’s motion and sunspots. Astron. J. 70, 193-200.

Kappraff, J. (1991): Connections – The geometric Bridge between art and science. New York, McGraw-Hill.

Keeling, C. D., Wharf, T. P., and the Carbon Dioxide Research Group (2003): Atmospheric CO2 concentrations (pomp) derived from in situ air samples collected at Mauna Loa, Hawaii.
http://cdiac.esd.ornl.gov/ftp/ndp001/maunaloa.co2.

Kolmogorov, A. N. (1979): Preservation of conditionally periodic movements with small change in the Hamiltonian function. Lecture Notes in Physics 93, 51.

Kuo, C., Lindberg, C., and Thompson, D. J. (1990): Coherence established between atmospheric carbon dioxide and global temperature. Nature 343, 709.

Landscheidt, T. (1983): Solar oscillations, sunspot cycles, and climatic change. In: McCormac, B. M., ed.: Weather and climate responses to solar variations. Boulder, Associated University Press, 293-308.

Landscheidt, T. (1984): Cycles of solar flares and weather. In: Moerner, N.A. und Karlén, W., eds..: Climatic changes on a yearly to millenial basis. Dordrecht, D. Reidel, 475, 476.

Landscheidt, T. (1986): Long-range forecast of energetic x-ray bursts based on cycles of flares. In: Simon, P. A., Heckman, G., and Shea, M. A., eds.: Solar-terrestrial predictions. Proceedings of a workshop at Meudon, 18.-22. Juni 1984. Boulder, National Oceanic and Atmospheric Administration, 81-89.

Landscheidt, T. (1987): Long-range forecasts of solar cycles and climate change. In: Rampino, M. R., Sanders, J. E., Newman, W. S. and Königsson, L. K., eds.: Climate. History, Periodicity, and predictability. New York, van Nostrand Reinhold, 421-445.

Landscheidt, T. (1988): Solar rotation, impulses of the torque in the Sun’s motion, and climatic variation. Clim. Change 12, 265-295.

Landscheidt, T.(1990): Relationship between rainfall in the northern hemisphere and impulses of the torque in the Sun’s motion. In: K. H. Schatten and A. Arking, eds.: Climate impact of solar variability. Greenbelt, NASA, 259-266.

Landscheidt, T. (1995): Die kosmische Funktion des Goldenen Schnitts. In: Richter, P. H., ed.: Sterne, Mond und Kometen. Bremen, Hauschild, 240-276.

Landscheidt, T. (1998 a): Forecast of global temperature, El Niño, and cloud coverage by astronomical means. In: Bate, R., ed.: Global Warming. The continuing debate. Cambridge, The European Science and Environment Forum (ESEF), 172-183.

Landscheidt, T. (1998 b): Solar activity - A dominant factor in climate dynamics. http://www.john-daly.com/solar/solar.htm

Landscheidt, T. (1999): Extrema in sunspot cycle linked to sun’s motion. Solar Physics 189, 415-426.
.

Landscheidt, T. (2000 a): Solar forcing of El Niño and La Niña. In: Vázquez , M. and Schmieder, B, ed.: The solar cycle and terrestrial climate. European Space Agency, Special Publication 463, 135-140.

Landscheidt, T. (2000 b): Solar wind near Earth: Indicator of variations in global temperature. In: Vázquez, M. and Schmieder, B, ed.: The solar cycle and terrestrial climate. European Space Agency, Special Publication 463, 497-500. 

Landscheidt, T. (2000 c): River Po discharges and cycles of solar activity. Hydrol. Sci. J. 45, 491-493.

Landscheidt, T. (2000 e): New confirmation of strong solar forcing of climate.    http://www.john-daly.com/po.htm.

Landscheidt, T. (2001 a): Solar eruptions linked to North Atlantic Oscillation. http://www.john-daly.com/theodor/solarnao.htm

Landscheidt, T. (2001 b): Trends in Pacific Decadal Oscillation subjected to solar forcing.
http://www.john-daly.com/theodor/pdotrend.htm.

Landscheidt, T. (2002): El Niño forecast revisited. http://www.john-daly.com/sun-enso/revisited.htm.

Landscheidt,T. (2003 a): Long-range forecast of U.S. drought based on solar activity.
       http://www.john-daly.com/solar/US-drought.htm

Landscheidt, T. (2003 b): New Little Ice Age instead of global warming. Energy and Environment 14, 4. 327-350.

Landsea, C. W. and Knaff, J. A. (2000): How much skill was there in forecasting El Niño? Bull. American Meteorol. Soc. 81, 2107-2119.

Mayaud, P. N. (1973): A hundred year series of geomagnetic data. IUGG Publication Office, Paris.

McKay, R. S., Meiss, J. D., and Percifal, I. C. (1987): Resonances in Hamiltonian maps. Physica D 27, 1.

Metzner, H. (1996): Gibt es einen CO2 – induzierten Treibhauseffekt? In: Metzner, H., ed.: Treibhauskontroverse und Ozonproblem. Europäische Akademie für Umweltfragen, Leipzig.

Moser, J. (1973): Stable and random motions in dynamical systems. Princeton Univ. Press.

Neelin, J. D. and Latif, M., 1998: El Niño dynamics. Physics Today, December 1998, 32-36.

Newman, M., Compo, G. P.,and Alexander, M. A. (2003): Enso-forced variability of the Pacific Decadal Oscillation. J. Climate Letters 16, 3853-3857.

Peixoto, J. P. and Oort, A. H., 1992: Physics of climate. New York, American Institute of Physics, 415-433.

Quinn, W. H., Neal, T. V., and de Mayolo, S. E. A. (1987): El Niño occurrences over the past four and a half centuries. Journ. Geophys. Res. 92, 14449-14461.

Ramage, C. S. (1986). El Niño. Scient. American , June 1986, 59-61.

Roederer, J. G. (1993): STEP and global change. STEP International 3(4), 4.

Sakurai, K. (1974): Physics of solar cosmic rays. University of Tokyo Press, 149.

Shindell, D., Rind, D., Balachandran, N., Lean, J., and Lonergan, P., 1999. Solar cycle variability, ozone, and climate. Science 284, 305-309.


Siegel, C. L. (1942): Iteration of analytic functions. Ann. Math. 43, 607-612.

Smith, H. J. and Smith, E. v. P. (1963): Solar flares. New York, MacMillan, 219.

Solar-Geophysical-Data (2003): < http://www.ngdc.noaa.gov/STP/SOLAR_DATA >

Sussman,G. J. and Wisdom, J. (1992): Chaotic evolution of the solar system. Science 257, 56-62.

Venables, W. N., and Ripley, B. D. (2002): Modern applied statistics with S. Springer, New York.

Von Storch, H. and Zwiers, F. W. (1999): Statistical analysis in climate research. Cambridge University Press, 294,296.

Walker, D. A. (1995): More evidence indicates link between El Niños and seismicity. EOS 76, No. 4, January 24, 1995, 33.

Walker, D. A. (1999): Seismic predictors of El Niño revisited. EOS 80, M0 25, June 22, 1999, 281.

Williams, N. R. (1977): Tornadoes, whirlwinds, and waterspouts. Encyclopaedia Britannica, Macropaedia, 18, 518.
 

Note - Dr Theodor Landscheidt makes the claim in the above paper that he predicted the last El Niño and La Niña two to three years before they actually happened.  I can confirm that the key paper in in which he predicted the 2002 El Niño and the preceding La Niña ("Solar Activity Controls El Niño and La Niña") , was published on this website in January 1999, fully three years before the actual event, and that the copy of that paper currently on this website is the original 1999 version. 
Signed - John L. Daly (19 Dec 2003)

Return to Climate Change Guest Papers Page

Return to  "Still Waiting for Greenhouse"  main page

FastCounter by bCentral