Introduction

The North Atlantic Oscillation (NAO) is one of the major modes of variability of the Northern Hemisphere atmosphere. It is a large scale see-saw in atmospheric mass between the subtropical high and the polar low exerting a strong control on winter climate in Europe, North America, and Northern Asia. The NAO index is defined as the normalized pressure difference between stations on the Azores and Iceland.

A positive NAO index indicates a stronger than usual subtropical high pressure center and a deeper than normal Icelandic low. The increased pressure difference results in more and stronger winter storms crossing the Atlantic Ocean on a more northerly track. This results in warm and wet winters in Europe and cold and dry winters in Greenland and Northern Canada, while the eastern United States experiences mild and wet winter conditions. A negative NAO index points to a weak subtropical high and a weak Icelandic low. The reduced pressure gradient results in fewer and weaker winter storms crossing mostly on west-east paths bringing moist air into the Mediterranean and cold air to Northern Europe. The east cost of the United States gets more cold air and snow while Greenland enjoys mild winters (Hurrell, 1995 ).

After ENSO, the NAO is one of the most dominant modes of global climate variability. Like El Niño, La Niña, and the Southern Oscillation, it is considered a free internal oscillation of the climate system not subjected to external forcing. It is shown, however, that it is closely linked to energetic solar eruptions. Surprisingly, it turns out that features of solar activity that have been shown to be related to El Niños and La Niñas (Landscheidt, 1999 a, 2000 a), also have an impact on the NAO.

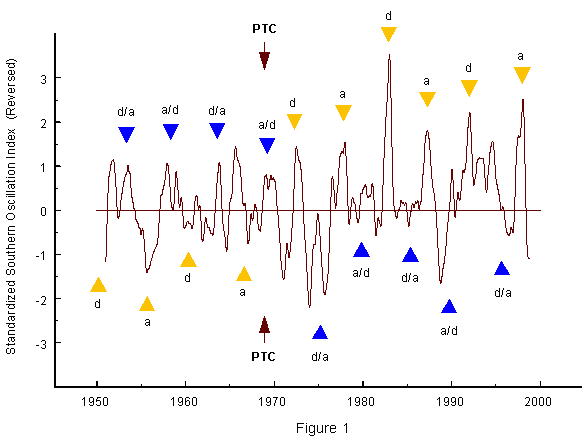
Fig.1 shows a close correlation between extrema in the Southern Oscillation Index (SOI), indicating ENSO events, and special phases a and d within the ascending and the declining part of the 11-year sunspot cycle. The SOI data are reversed so that strong positive peaks point to El Niños and troughs to La Niñas. The 11-year cycle is not symmetric. Reliable observations available since 1750 show that the mean rise to the sunspot maximum (4.3 years) is considerably steeper than the decline to the sunspot minimum (6.7 years). The mean ratio of the rising part to the whole 11-year cycle is 0.39. 

Nature often repeats patterns and connected functions on different scales. The phases indicated in Fig.1 by triangles represent such fractals. Yellow triangles mark points a and d which divide the ascending and the descending part of the sunspot cycle such that the ratio 0.39, found in the whole cycle, is again established in the respective parts. It should be noted that point 0.39 in the 11-year cycle coincides with the sunspot maximum, a climax of activity. Points a and d seem to have a similar function. Midpoints between phases a and d (a/d and d/a), marked by blue triangles, are farthest away from points a and d. So it is consistent that they indicate the opposite effect.  After 1970, on the right of the two arrows labelled PTC (Perturbation in torque cycle), all yellow triangles point to El Niños and all blue triangles to La Niñas. Before 1970, everything is reversed. As this conspicuous pattern is linked to the Sun's activity, which again is based on the Sun's dynamics, an explanation of the phase reversal, too, should be found in the Sun's dynamics. I have shown that there are torque cycles in the Sun's oscillation about the center of mass of the solar system which are associated with solar activity (Landscheidt, 1986 a, b, 1999 b ) and climate change (Landscheidt, 1983, 1987, 1988, 1990, 1995, 1998 a,b, 2000 c ).

On this basis, I correctly predicted energetic solar eruptions, strong geomagnetic storms, weaker solar activity past 1990, the end of the Sahelian drought, extrema in global temperature anomalies, drought conditions in the United States, and the last two El Niños 1 to 4 years before the events. The forecast of solar eruptions and geomagnetic storms, checked by astronomers and the Space Environment Center, Boulder, covered six years and achieved a hit rate of 90 %. 

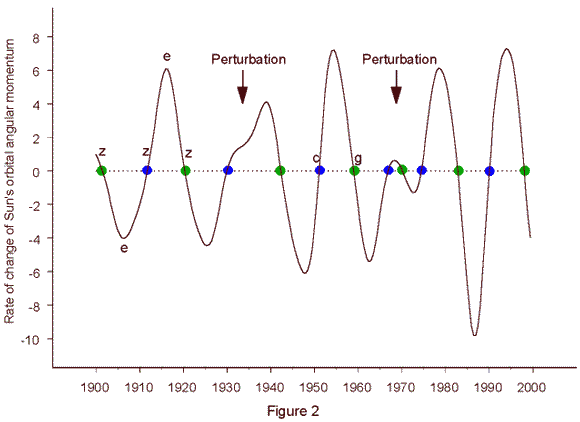
Fig. 2 shows that the rate of change of the Sun's orbital angular momentum (L) - the torque dL/dt driving the Sun's motion about the center of mass of the solar system - forms a torque cycle of varying length. The initial phases of this cycle are marked by blue circles. Perturbations in the sinusoidal course of the torque cycle, indicated by arrows, occurred around 1933.6 and 1968.8. Such events recur at quasi-periodic intervals and mark initial phases of a perturbation cycle of 35.8 years. Observation shows that such predictable perturbations release phase reversals and other disturbances in cycles of climate phenomena connected with the Sun's activity (Landscheidt, 1995, 1998 a, b). The perturbation in the torque cycle that occurred around 1968 falls just at the phase reversal in the correlation pattern presented in Fig.1. 

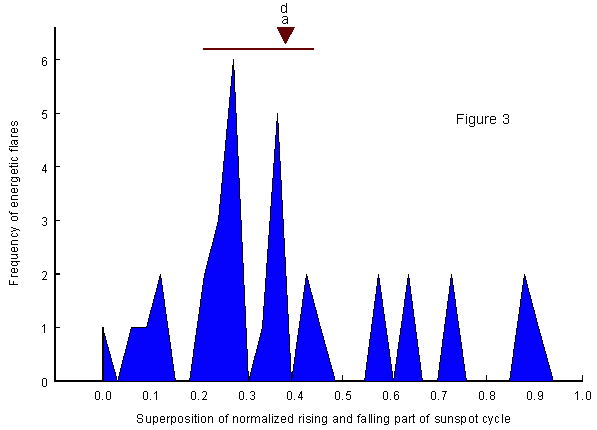
Fig 3 shows why just phases a and d within the ascending and the descending part of the 11-year sunspot cycle could be related to ENSO events. It shows the distribution of highly energetic X-ray flares within the respective parts of the sunspot cycle. The sample covers all X-class flares equal to or greater than 6 observed by satellites between 1970 and 2000. These data are available at the National Geophysical Data Center, Boulder. The rising and falling parts of different length were normalized to have equal length 1. Then they were superimposed to make it easy to recognize identical phases. Intense X-ray flares, nearly always accompanied by heavy coronal mass ejections, are geophysically more effective than flares categorized into classes of optical brightness (Joselyn, 1986). As many as 19 of the 34 investigated X-ray flares concentrate on the short interval of 0.23 on the unit scale, marked by a horizontal bar at the top left. Only 15 of the flares fall at the remaining large interval covering a range of 0.77 on the unit scale. The normalized position of a and d is marked by a brown triangle. The climate effect, observed at a and d, lags the eruptions, the conceivable cause.

Statistically, the flare accumulation is highly significant. Even when compared with the distribution of mean counts of grouped optical flares, bootstrap resampling and randomization tests show that the probability of a false rejection of the sceptic null hypothesis is much smaller than 0.01. Highly energetic cosmic ray flares observed between 1942 and 1970 (Sakurai, 1974) corroborate this result. As to a potential physical background of the link between energetic solar eruptions and ENSO events I refer to "Solar Forcing of El Niño and La Niña" (Landscheidt, 2000 a ) and "Solar Activity Controls El Niño and La Niña" (Landscheidt 1999 a).
 
 

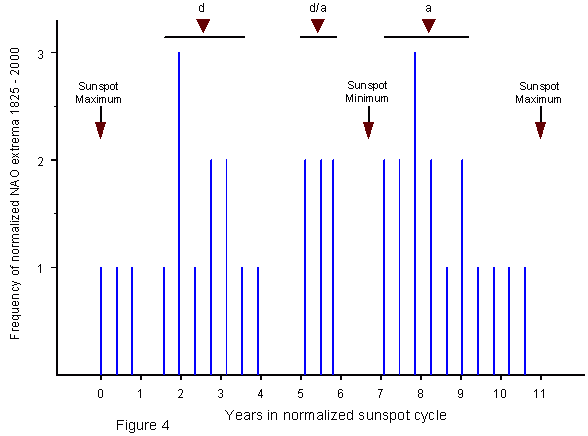
NAO extrema and phases a and d in sunspot cycle

The Southern Oscillation and the North Atlantic Oscillation are comparable climate phenomena though located in different world regions. So I adopted the working hypothesis that the NAO, if subjected to solar forcing, would be related to the same phases of eruptional activity within the 11-year sunspot cycle as ENSO events. To test this hypothesis, I investigated yearly means of the NAO index covering 1825 to 2000.  Jones et al. (1997) used early instrumental data to extend the index back to 1825.  These data are available at the Climate Research Unit of the University of East Anglia (2001). When I subjected the time series to 5-year moving window Gaussian kernel smoothing (Lorczak), the smoothed curve displayed 36 extrema (maxima and minima). I related the dates of these NAO extrema to the respective sunspot cycles normalized to 11 years. An analysis of the normalized positions of the extrema within the 11-year cycle showed that just the points a, d, a/d, and d/a, which play a major role in the relationship with ENSO events, show a close connection with NAO extrema when the data are shifted to offset a 1.5-year lag of the NAO maxima and minima. As to ENSO events in the Pacific, such lags reach at most a few months. A wider lag in the North Atlantic is acceptable as its location is far north of the equator where El Niño and La Niña develop in a climate with a much higher energy potential. Thermal inertia of the oceans and marine currents may be involved. 

White et al. (1997) have shown how the oceans respond to excess insolation caused by solar forcing and why there can be a lag of several years depending on the length of the involved cycles of solar activity.  Fig. 4 shows the result of the test.

The vertical axis indicates the frequencies with which NAO extrema fall in bins with 0.4-year class intervals. The normalized 11-year sunspot cycle runs from maximum to maximum. Phases a, d, and d/a are marked by triangles. Point a/d nearly coincides with the sunspot maximum. The NAO extrema accumulate around the crucial phases. Out of 36 maxima and minima as many as 33
fall at the intervals marked by horizontal bars at the top and a short range before and after the sunpot maximum. The total range covers 6.3 out of 11 years.

A Pearson-test covering 2 classes (1 degree of freedom) yields the chi-square value 17.4 and P=0.00003. The probability of a false rejection of the sceptical null hypothesis is only one in 33333. It cannot be objected that the shift to offset the lag manipulates the data to get a significant result. When the data are tested without any shift, there are already non-random accumulations at similar intervals that go beyond the significance level 0.002. This pattern only stands out more distinctly after the shift. It should be noted that the 1.5-year shift affects the position of a in the ascending part of the sunspot cycle much stronger than the position of d in the descending part, as the mean length of the ascending part is only 4.3 years. To get special manipulated  results under such conditions would be extremely difficult.

Fig. 5 shows the course of yearly NAO anomalies normalized to the standard deviation for the period 1950 - 2000. The yearly values were taken from the time series subjected to 5-year moving window Gaussian kernel smoothing (Lorczak). It can be seen in detail that the crucial phases are closely connected with NAO extrema. The perturbation in the torque cycle (PTC) in 1968.8, indicated by an arrow, initiated a disturbance, though different from the ENSO pattern in Fig. 1. The connection of a and d with NAO minima and maxima was interrupted and switched to midpoints a/d and d/a which replaced phases a and d. Yet this change did not last long. After a decade, the former pattern re-emerged. Though the NAO data in Fig. 5 were not shifted, the respective extrema closely coincide with the activity phases.

This seems to contradict the results in Fig. 4 based on a 1.5-year shift. The explanation is that the extension of the lags depends on the level of solar activity.  From 1875 to 1945, while the sunspot activity was low or very low, the NAO constantly lagged the activity phases by about 1.5 years, whereas the period of high solar activity from 1947 to 1996 seems to have accelerated the solar effect. As to eruptional activity, solar cycle No. 22, running from 1986.7 to 1996.4, was one of the most active, or even the strongest ever observed (Landscheidt 1999 b). The ascending part of the cycle had a very short length of no more than 2.8 years. This could explain that during this cycle the NAO response was accelerated to such a degree that the extrema occurred already before points a and d. The next phase d is to be expected in 2003.2.
 
 

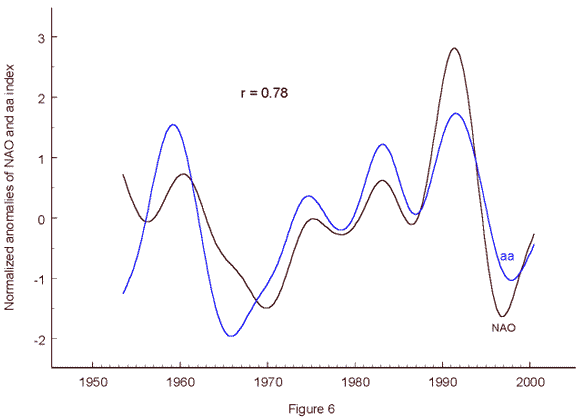
NAO data and geomagnetic aa index

Not all strong solar eruptions have an impact on the near-Earth environment. The effect at Earth depends on the heliographic position of the eruption and conditions in interplanetary space. Indices of geomagnetic activity measure the response to those eruptions that actually affect the Earth. Mayaud's aa index (Mayaud, 1973) is homogeneous and covers a long period. So I compared it with the NAO data. I chose the period 1953 to 2000 as I wanted to extend the comparison to galactic cosmic rays (GCR) for which neutron measurements are available since 1953. Figure 6 shows the result.

The blue curve represents anomalies of the aa index, smoothed and normalized to the standard deviation like the NAO index. The brown curve displays the NAO data. The two time series are well correlated. The correlation coefficient is as high as r = 0.78 and explains 61% of the variance. Though there is a well established reciprocal physical link between the aa index and galactic cosmic rays, their correlation coefficient for the same period is only slightly higher: r = -0.82. Bootstrap resampling, making use of up to a million samples drawn at random from the observed set, shows clearly that the significance of r = 0.78 is so high that there is not even one chance in a million to falsely reject the sceptic null hypothesis.  Between 1964 and the early seventies, the correlation is weaker than after this period.  This concurs with an intermittent phase of weaker solar activity.  The sunspot maxima 1947.5, 1957.9, 1979.9, and 1989.5 were all beyond R=150, whereas the maximum 1968.9 reached only R=106. For the period of high solar activity from 1970 to 2000 the correlation coefficient for aa and NAO rises to r = 0.93. Even the physically explained negative correlation between aa and GCR is not as high in this period: r = -0.88. This shows again that the level of solar activity is an important factor in the investigated relationship.
 
 

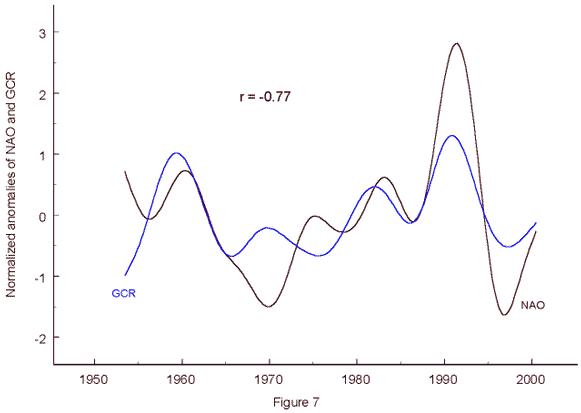
NAO index and cosmic rays

The extent of cloud cover has a strong impact on temperature and climate, especially over the oceans. Clouds are on average about 10°C colder than the surface and reflect between 20 and 30 % more sunlight. Over the oceans, 67% of the sky is cloudy and more than half of that area densely overcast.  Only 15% of the continents, however, is thickly blanketed. Svensmark and Friis-Christensen (1997) and Svensmark (1998) have shown that global cloud cover over the oceans, observed by satellites, is linked to variations in the flux of cosmic rays modulated by the solar wind. This effect is attributed to cloud seeding by ionized secondary particles.  Stronger cosmic rays are expected to extend the cloud cover, whereas weak cosmic rays, kept at bay by strong solar wind, go along with shrinking clouds.

New results published by and Pallé Bagó and Butler (2000 a, b) and Marsh and Svensmark (2000) restrict the relationship to low clouds. Dense sheets of stratocumulus clouds hanging just above the oceans cool more than they heat. If such sheets shrink, it gets warmer. The cloudiest regions are in the temperate zones. As atmospheric temperature and pressure are related, it is imaginable that there is a connection between cosmic ray variations, cloud cover over the Atlantic, and the North Atlantic Oscillation. Fig. 7 shows that there is a close correlation between cosmic rays and the NAO index.

The blue curve displays smoothed normalized anomalies of yearly mean values of GCR data observed by the Huancayo Neutron Monitor (Solar-Geophysical Data, 1999) since 1953. The data are reversed to make it easier to judge the degree of a potential negative correlation. The already investigated aa index and cosmic rays show a negative correlation because of the shielding effect of the solar wind driven by solar activity. The brown curve plots the NAO data. The strong negative correlation (r = - 0.77) is obvious. It explains 59% of the variance. Interestingly, just during the weak sunspot cycle running from 1964 to 1976 the correlation displayed a strange pattern. A phase reversal occurred that inverted the negative correlation temporarily to a positive one. This changed again when the following strong sunspot cycle developed. This feature could be of importance in attempts to find a detailed physical explanation of the connection.
 
 

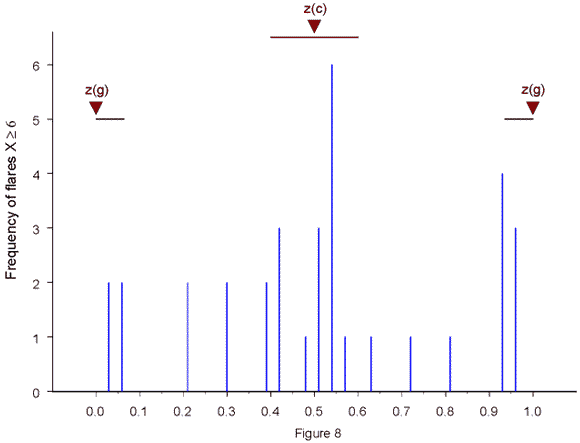
Torque cycle in the Sun's motion, solar eruptions, and NAO extrema

I have shown that zero phases of the torque cycle in the Sun's motion, visible in Fig. 2, are linked to ENSO events (Landscheidt, 1999 a).  In view of the results with phases a and d in the sunspot cycle, there seem to be good reasons to expect a similar connection with the NAO. Zero phases (z), as marked in Fig. 2, do not only comprise initial phases (blue), but also phases pi (green) initiating the second half of the respective cycle. A growing body of evidence suggests that zero phases in the torque cycle have an impact on weather and climate because they go along with accumulations of energetic solar eruptions. I have tried to draw attention to this special relationship since 1976 (Landscheidt, 1976). Fig. 8 shows a new result. 

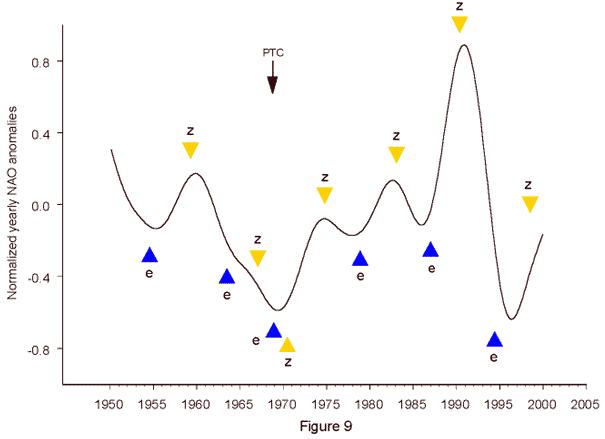
The two types of zero phases in the torque cycle have different physical functions. They are indicated in Fig. 2 by labels c and g. Phase c (blue) initiates an increase in orbital momentum resulting in centrifugal motion of the Sun away from the center of mass. Phase g (green) starts a decrease in orbital momentum resulting in centripetal motion toward the center of mass due to prevailing gravitation in the difference forces. In both of these cases the zero phases start an impulse of the torque in the Sun's motion. The different types c and g could have different effects on the Sun's activity and solar-terrestrial interaction. So I distinguished zero phases c and g in an investigation into their relationship with solar eruptions.

Figure 8 shows the frequency distribution of powerful X-class flares, already analysed in Fig. 3, within a normalized interval from one zero phase g (z(g)), marked by a triangle, to the next one. The normalized position of zero phase c (z(c)) in between is also indicated by a triangle.The strong X-ray flares concentrate before and after z(g) and around z(c). As many as 27 of the investigated 34 flares concentrate on the short intervals marked by horizontal bars at the top comprising a total of 0.35 on the scale normalized to 1. Only 7 of the flares fall at the remaining interval of 0.65 on the unit scale. A Pearson-test covering two classes (1 degree of freedom) yields the chi-square value 29.5 and P = 0.00000006. The null hypothesis of no correlation is disproved at a level of significance rarely found in such small samples. In addition, there are aggregations around 0.25 and 0.75 on the unit scale.

This would be the normalized positions of the torque extrema labelled e in Fig. 2.  Contrary to expectation, the concentrations of flares around phases z(g) and z(c) show no significant difference in their frequencies in spite of their different physical functions. Solar eruptions are caused by instability on the Sun. It could be that they are linked to instability in the solar motion cycle. As stated by chaos theory, instability is the characteristic mark of all zero phases that are sites of boundary transitions from one polar quality to the opposite one, as for instance from centrifugal force to gravitation, or vice versa. Extrema in cycles are similar sites of instability. For a moment the quantities involved stop to grow in the positive or negative direction and then switch to the opposite direction. If this were crucial, it should make no difference whether the extremum is positive or negative. I found just this in a time series of River Po discharges linked to a torque cycle formed by the absolute rate of change | dL/dt | in the Sun's orbital angular momentum L (Landscheidt, 2000 b). These cycles do not run from initial phase c to the next one, but from z to z.

The connection proved dependable, as the forecast of a maximum of the discharges in the River Po catchment area around 2001.1, based on an absolute extremum in the torque cycle, turned out correct (Landscheidt, 2000 d). After a protracted dry period, the predicted wet period was initiated by severe floods in Northern Italy that began in October 2000. The wet climate continued till spring 2001. Climate in the Mediterranean is known to be connected with the NAO (Tomasino and Dalla Valle, 2000). So I hypothesize that all phases z in the torque cycle, irrespective of their different physical background, and all extrema e, independent of their sign, show a similar relationship with extrema in the NAO data like phases a, d, a/d, and d/a in the sunspot cycle. Fig. 9, a reprise of Fig. 5, confirms this working hypothesis. 

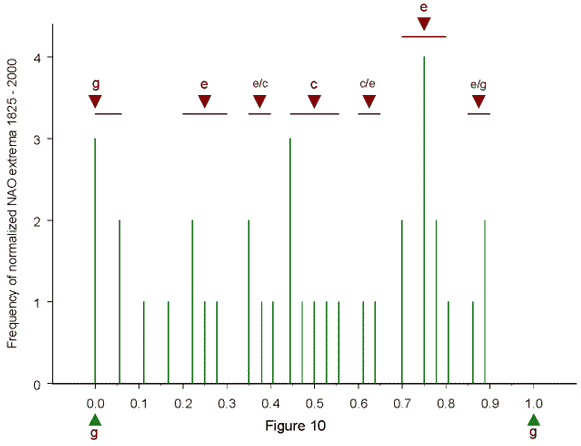
As surmised, extrema e play an important role besides zero phases z. Contrary to all other cases, phases e and z in 1963.0 and 1967.1 are not related to well developed NAO extrema. There are only slight disturbances in the course of the NAO curve that indicate a tendency in the respective direction. This seems to be related to the proximity of the perturbation PTC in 1968.8, indicated by an arrow.  Just the same happened before the preceding PTC in 1933.6. The disturbance in the torque cycle also explains a phase shift in the z phase 1970.5, the only exception in the otherwise consistent pattern. Phase e in 1994.4 seems rather far from the NAO minimum 1996, but this will be explained later when dealing with Fig. 11.

The NAO data in Fig. 9 were not shifted as they cover a period of high solar activity. I hypothesized, however, that an investigation of the whole data set, including long periods of weak solar activity, would show that the NAO extrema lag z and e on average by 1.5 years like a and d . Fig. 10 shows how the NAO extrema are distributed within intervals g to g normalized to 1 from 1825 to 2000 when they are shifted to offset a 1.5-year lag.

As postulated, the extrema concentrate at g and around c and e. Surprisingly, the analysis reveals that 4th harmonics of the |dL/dt|-cycle are also involved.  The respective harmonics are labelled e/c, c/e, and e/g. For short, they will be called phases m because they appear at midpoints between normalized phases z and e. A closer look shows that 4th harmonics only emerge in very long z - z intervals. Between 1819.4 and 2008.4 the longest |dL/dt| cycle has a length of 14.8 years while the shortest one has a length of 2.6 years.  In the period 1950 to 2000, covered in Fig. 9, there are no unusually long cycles. The active phases in the g - g interval in Fig. 10 are precisely connected with the investigated NAO extrema. The range of effectiveness around e/c, c/e, and e/g is only half as wide as around g, c, and e. Out of 36 NAO extrema as many as 32 fall at the ranges marked by horizontal bars at the top of Fig. 10 covering a total range of 0.54 on the unit scale. Only 4 extrema fall at the space in between the active phases.

A Pearson-test covering 2 classes (1 degree of freedom) yields the chi-square value 18.1 and 
P = 0.00002. The probability of a false rejection of the null hypothesis is very small. If a range for the only omitted harmonic g/e is inserted, though there is no aggregation of NAO extrema, the chi-square value is still 16.2 with P = 0.00006.
 
 

Accumulation effect and forecast potential

Fig. 11 shows the combined effect of z and e (blue triangles) and of a, d, a/d, and d/a (yellow triangles) on NAO extrema. Obviously, maxima or minima occur when elements of the two different sets coincide within a relatively small range. The data were not shifted, as the period 1950 - 2000 is characterized by a high level of solar activity. Phases m do not emerge as the intervals z - z falling in this period are rather short, the longest one being 8.3 years.

The deep NAO minimum in 1969 is not only unusual in so far as it goes along with a PTC disturbance and a phase reversal in the zero phase 1970.5. Another distinguishing feature is the cluster of three phases with e and z exceptionally close together. Around the NAO minimum 1996, e and a are farther away from the mark than any of the phases that indicate NAO extrema. Yet the midpoint in between, indicated by an open triangle, coincides nearly exactly with the NAO minimum. If this is a valid feature, another NAO extremum should be expected around 2004.5, as indicated by an open triangle between d (2003.2) and z (2005.8) on the right hand side of Fig. 11.  Under the prevailing circumstances the extremum will probably be a maximum.

Fig. 12, covering the years 1900 - 1950, confirms the result shown in Fig.11 that NAO extrema occur when phases of the different sets coincide within a small range.  Nearly all single phases, indicated by green circles, are far from maxima or minima in the NAO data. There is only one exception. The second maximum from the left is related to a single phase z. Yet this maximum is the smallest in the investigated period. The decades after the disturbances PTC 1900 and PTC 1933.6 are the only ones with emerging phases m and d/a. As stated before, phases m only occur within long intervals z - z. In the present case, the respective |dL/dt| cycles have lengths of 10.3 and 12.4 years. As before PTC 1968.8, coinciding phases a and e before PTC 1933.6 are not linked to a fully developed extremum. The analysis covers a period of solar activity that was weak or very weak up to the sunspot minimum 1944.2.  So the marks of the phases were shifted to offset the 1.5-year lag. Only the phase close to the high sunspot maximum 1947.5 was not shifted.  Taken together, the presented results show that it is possible to develop a long-range forecast of NAO extrema.
 
 

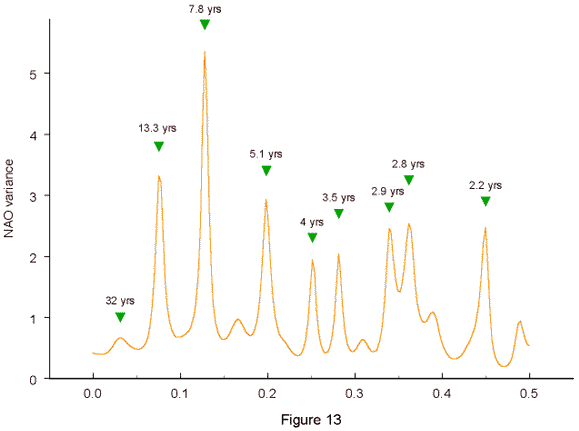
Frequency spectrum analysis

Most climatologists think that frequency analyses of NAO indices - unlike ENSO - yield broad band spectra with no significant dominant periodicities and no relationship with natural cycles.  The maximum entropy spectrum (Burg, 1975) in Fig. 13, based on raw yearly data of the NAO index 1825 - 2000, disproves this assumption. 

To avoid spectrum instability, a filter length of 40 coefficients was chosen, less than 25% of the 176 data points. The results were checked by a Blackman-Tukey power spectrum (Blackman and Tukey, 1959). The outstanding peak at 7.8 years nearly exactly matches the mean length 7.86 years of the |dl/dt| cycle (z - z) measured in the investigated period 1825 - 2000.  Actually, the interval 1819 - 2008 was chosen to cover complete cycles.  The main peak is highly significant.  An acknowledged reliability test of spectral peaks does not exist for the maximum entropy method.  It is available, however, for the Blackman-Tukey power test.

Though it allows for Markov red noise in natural time series, the level of significance is far beyond 0.01.   The mean distance of phase d from the sunspot minimum, the beginning of the sunspot cycle, is 6.8 years. The strong peak at 13.3 years is close to the second sub-harmonic 13.6 years of this basic distance. The third strong peak at 5.1 years points to the mean interval a - d of 5. 2 years. The second harmonic of the main peak 7.8 years is at 3.9 years.  It is explained by the mean distance between z and e or e and z, which is 3.9 years. The peak at 4 years is rather close to it. The rest of the peaks shows similar relationships. The second harmonic of the distance of phase d from the sunspot minimum at 3.4 year is indicated by the peak at 3.5 years.  The peak at 2.9 years points at the second harmonic 2.9 years of the distance d - a, which is 5.8 years.  The distance from a/d to d/a is 5.5 years. Its second harmonic 2.8 years is related to a peak at just this wavelength. The last distinct peak at 2.2 years could point to the Quasi-Biennial Oscillation with a mean length of 2.2 years, but it is also close to the mean distance 2 years separating phase m from z and e.

All of these peaks are confirmed by the Blackman-Tukey power spectrum and turn out to be significant at least at the level 0.05. Interestingly, the low peak at 32 years on the left hand side of Fig. 13, the only one that points to a cycle of several decades, points at the fourth sub-harmonic 31.4 years of the mean interval z - z represented by the main peak.  So there are solid indications that the prominent frequency peaks are real and closely connected with the solar phases in question. 
 
 

Outlook

Taken together, the presented lines of evidence leave little doubt that there is a solid link between solar eruptions, eruptive phases in the 11-year sunspot cycle, zero phases and extrema in the solar motion cycle formed by | dL/dt |, and extrema in the NAO data. This opens up new vistas of research, as it has been a tenet of climatology that the Northern Atlantic Oscillation is an internal process in the atmosphere-ocean system not subjected to external forcing.  Moreover, the results show clearly that contrary to statements of the IPCC and assertions in the literature (Tett et al., 1999) solar forcing on climate phenomena did not fade away in recent decades.  Predictability is one of the corner stones of science.  The predictive potential of the upshot is obvious, though the patterns are not as stable as the patterns that make it possible to predict ENSO events.  An explanation could be that El Niño and La Niña develop in an environment with a much higher energy potential. 

Admittedly, the mechanisms that create such strong solar forcing remain poorly understood in detail.  Yet this situation is not new in the history of science.  Epistemologically, the stages of gathering data, establishing morphological relationships, and setting up working hypotheses necessarily precede the stage of elaborated theories.  We are able already to discern simple underlying patterns in a seemingly impenetrable thicket of data without correlations.  If the fields of solar activity and climatic change shape well and develop into full-fledged theories, it is conceivable that the semi-quantitative model presented here will be better understood in the new theoretical environment. The present results are only first tentative steps in a new direction.  There are many problems that can only be solved by a joint interdisciplinary effort of open-minded scientists.

References

Blackman, R. B. and Tukey, J. W. (1959): The measurement of power spectra. Dover, New York.

Burg, J. P. (1975): Maximum entropy analysis. Ph. D. thesis. Stanford University, Palo Alto.

Climate Research Unit of the University of East Anglia (2001):   http://www.cru.uea.ac.uk.

Hurrel, J. W. (1995): Decadal trends in the North Atlantic Oscillation and relationships to regional temperature and precipitation. Science 269, 676-679.

Jones, P. D., Jonsson, T., and Wheeler, D. (1997): Extension to the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and South-West Iceland. Int. J. Climatol. 17, 1433-1450.

Joselyn, J. A., (1986): SESC methods for short-term geomagnetic predictions. In: Simon, P. A. et al., eds.: Solar-Terrestrial Predictions. Boulder, NOAA, 405.

Landscheidt, T. (1976): Beziehungen zwischen der Sonnenaktivität und dem Massenzentrum des Sonnensystems. Nachrichten der Olbers-Gesellschaft 100.

Landscheidt, T. (1983): Solar oscillations, sunspot cycles, and climatic change. In: McCormac, B. M., ed.: Weather and climate responses to solar variations. Boulder, Associated University Press, 293-308.

Landscheidt, T. (1986 a): Long-range forecast of energetic x-ray bursts based on cycles of flares. In: Simon, P. A., Heckman, G. und Shea, M. A., eds.: Solar-terrestrial predictions. Proceedings of a workshop at Meudon, 18.-22. Juni 1984. Boulder, National Oceanic and Atmospheric Administration, 81-89.

Landscheidt, T. (1986 b): Long-range forecast of sunspot cycles. In: Simon, P. A., Heckman, G. und Shea, M. A., eds.: Solar-terrestrial predictions. Proceedings of a workshop at Meudon, 18.-22. Juni 1984. Boulder, National Oceanic and Atmospheric Administration, 48-57.

Landscheidt, T. (1987): Long-range forecasts of solar cycles and climate change. In: Rampino, M. R., Sanders, J. E., Newman, W. S. und Königsson, L. K., eds.: Climate History, Periodicity, and predictability. New York, van Nostrand Reinhold, 421-445.

Landscheidt, T. (1988): Solar rotation, impulses of the torque in the Sun's motion, and climatic variation. Climatic Change 12, 265-295.

Landscheidt, T.(1990): Relationship between rainfall in the northern hemisphere and impulses of the torque in the Sun's motion. In: K. H. Schatten and A. Arking, eds.: Climate impact of solar variability. Greenbelt, NASA, 259-266.

Landscheidt, T.(1995): Global warming or Little Ice Age? In: Finkl, C. W., ed.: Holocene cycles. A Jubilee volume in celebration of the 80th birthday of Rhodes W. Fairbridge. Fort Lauderdale, The Coastal Education and Research Foundation (CERF), 371-382.

Landscheidt, T. (1998 a): Forecast of global temperature, El Niño, and cloud coverage by astronomical means. In:Bate, R., ed.: Global Warming. The continuing debate. Cambridge, The European Science and Environment Forum (ESEF), 172-183.

Landscheidt, T. (1998 b): Solar activity : A dominant factor in climate dynamics. 
http://www.john-daly.com/solar/solar.htm.

Landscheidt, T. (1999 a): Solar activity controls El Niño and La Niña
http://www.john-daly.com/sun/sun-enso.htm

Landscheidt, T. (1999 b): Extrema in sunspot cycle linked to Sun's motion. Solar Physics 189, 413-424.

Landscheidt, T. (2000 a): Solar forcing of El Niño and La Niña. ESA Special Publication 463, 135-140.

Landscheidt, T. (2000 b): River Po discharges and cycles of solar activity. Hydrol. Sci. J. 45, 491-493.

Landscheidt, T. (2000 c): Sun's role in the satellite-balloon-surface issue. 
http://www.john-daly.com/solar/temps.htm

Landscheidt, T. (2000 d): New confirmation of strong solar forcing of climate.
http://www.john-daly.com/po.htm

Marsh, N. D. and Svensmark, H. (2000): Low cloud properties influenced by cosmic rays. Phys. Rev. Lett 25, 5004.

Mayaud, P. N. (1973): A hundred year series of geomagnetic data. IUGG Publications Office, Paris.

Pallé Bagó, E. and Butler, C. J. (2000 a): The influence of cosmic rays on terrestrial clouds and global warming. Astron. Geophys. 41, 4.18-4.22.

Pallé Bagó, E. and Butler, C. J. (2000 b): Sunshine, clouds, and cosmic rays. ESA Special Publication 463, 147-152.

Sakurai, K. (1974): Physics of solar cosmic rays. Tokyo, University of Tokyo Press, 149.

Solar-Geophysical Data. NOAA Geophysical Data Center. Boulder, Prompt Reports, August 1999, 180.

Svensmark, H. and Friis-Christensen, E. (1997): Variation of cosmic ray flux and cloud coverage: A missing link in solar-terrestrial relationships. J. Atmosph. Sol. Terr. Phys. 59, 1225-1232.

Svensmark, H. (1998): Influence of cosmic rays on Earth's climate. Phys. Rev. Lett. 81, 5027-5030.

Tett, S. F. B., Stott, P. A., Allen, M. R., Ingram, W. J., Mitchell, J. F. B. (1999): Causes of twentieth-century temperature change near the Earth's surface. Nature 399, 569-572.

Tomasino, M. and Dalla Valle, F. (2000): Natural climatic changes and solar cycles: An analysis of hydrological time series. Hydrol. Sci. J. 45 (3), June 2000.

White, W. B., Lean, J., Cayan, D. R., Dettinger, M.D. (1997): Response of global upper ocean temperature to changing solar irradiance. J. Geophys. Res. 102, 3255-3266.