Absorption
of Carbon Dioxide
from the Atmosphere
by
Dr. Jarl Ahlbeck
A chemical engineering view of a fullscale carbon dioxide absorber. Special report for the website www.john-daly.com with thanks to John Daly for the efficient information service and his contribution to the modern critical scientifical discussions on the net. Although this report contains some mathematical formulas that may be difficult to understand for many people, I have tried to explain the main points in the text as clearly as possible.
Dr. Jarl Ahlbeck (D.Sc., Chem.Eng., Research Associate)
I am a 52 yr old consulting scientist and lecturer in environmental engineering at the Swedish university of Finland, Abo Akademi University, Process Design Laboratory. During my 27 years as active consulting chemical engineer I have worked with applied mathematical modeling of industrial absorption, desorption, stripping, drying, flue gas desulfurization, supercritical extraction and industrial waste water cleaning. My special interest is mathematical statistics, experimental design and statistical process- and quality control.
![]()
![]()
Abstract
Analysis of data published by the CDIAC (1999) for anthropogenic emissions of carbon dioxide from fossil fuels and cement industry for the period 1960-1997 together with measured values of the atmospheric carbon dioxide concentration, indicates that the net sink flow rate, or the uptake rate of anthropogenic carbon by the biosphere and the oceans, is primarily controlled by the concentration of carbon dioxide in the atmosphere. This means that the "consensus" carbon cycle models (IPCC 1996) seem to overpredict the future atmospheric carbon dioxide concentration to a great extent.
Introduction
In my report on this website, "The IPCC Carbon Dioxide Predictions are Erroneous", I have showed that the computerized carbon cycle model used by the IPCC (1996), the "Bern" model, gives results that are in good agreement with a very trivial assumption of a constant value of the "airborne fraction" which is the fraction of the anthropogenic carbon dioxide emission that stays in the atmosphere. This means that the emitted carbon dioxide is directly "partitioned amongst reservoirs" in proportions predicted by the model. This is easily obtained from the Technical Summary, Table 2 at page 17, Figures 5 (a) and 5 (b) at page 23 (IPCC 1996).
I discovered last year that the same resulting atmospheric CO2 concentrations for the period 2000 - 2100 that have been calculated by the computerized "Bern" carbon cycle model from different scenarios, can easily be calculated by hand in a few minutes directly from the given scenarios simply by using a value of the airborne fraction of 0.5.
A constant value of the airborne fraction is theoretically possible only if the atmosphere-ocean surface-biosphere system works as an ideally closed and backmixed batch-absorber which equilibrium concentrations according to Henry's law.
According to the IPCC-model, we do not live in a yellow submarine, we all live in a bottle of beer.
The IPCC carbon cycle modelers claim (personal communication on the Net) that they never have considered the airborne fraction as a constant in their sophisticated computerized carbon cycle models. But they cannot deny the fact that their published calculated predictions can be very exactly reproduced simply by putting a constant value of the airborne fraction into a trivial mass balance.
Basic carbon cycle assumptions
The modelers partition the anthropogenic carbon dioxide here and there amongst different reservoirs. The most important reservoir is the backmixed surface layer of the ocean. The further transport of anthropogenic carbon from the surface to the ocean bulk is believed to be extremely slow. The anthropogenic emissions are added to the gas phase of the batch (the atmosphere), continuously increasing the equilibrium carbon content of the surface layer as a result of the increasing partial pressure of the carbon dioxide in the gas phase.
According to Jain, et al., (1995), and Siegenthaler and Joos (1992) ocean chemistry and vertical mixing processes are explicitely computed using a "one-dimensional upwelling-diffusion model or a variant of it". As usual, the details of the computer programs are known only by the programmers themselves.
The "Bern" model has been tested by comparing the calculated carbon dioxide profiles with the observed oceanic profiles of C-14 following nuclear bomb testing. Unfortunately this test is not relevant for testing the calculation of the net sink flow of anthropogenic carbon by the model because the influence of recently increased partial pressure of atmospheric carbon dioxide cannot be checked in that way. The distribution of C-14 in different ocean layers may however be interesting as a study of how individual carbon dioxide molecules are mixed into the ocean at various depths.
A chemical engineering mass balance for a carbon dioxide absorber
Let's look upon the atmosphere-ocean-biosphere system as a little more complicated industrial carbon dioxide batch absorber than an ideally backmixed bottle. Our planet contains an upper well-mixed air phase (the atmosphere) and a huge bulk of absorbent, a salt solution (the ocean). To the gas phase a small flow of additional carbon dioxide is blown (the anthropogenic emissions). In the gas phase some green stuff is planted (the biosphere).
The surface of the absorbent is mixed by a stirrer or a surface areator of the same type as used in waste water cleaning plants. The mixer influences the bulk efficiently by strong primary mixing to only about 3 % of the total depth (the backmixed layer). Due to secondary currents the concentration gradients cause diffusional mass transfer from the saturated (equilibrated) surface water to the huge liquid bulk of absorbent salt solution.
A part of the additional carbon dioxide that we put into the absorber is absorbed in the surface layer whose chemical composition fastly achieves chemical equilibrium with the gas phase. Because the diffusional transport of the dissoluted carbon dioxide to the bulk of the absorbent is slow and and the capacity of the backmixed layer to store carbon dioxide is limited, carbon dioxide is continuously enriched in the gas phase. The concentration in the gas phase increases gradually. The green stuff absorbs carbon dioxide, the higher the partial pressure is, the more is absorbed.
A mass balance for the anthropogenic carbon flow rate can we written according to
![]()
where the anthropogenic emission flow rate of carbon, Fem is accumulated in the back-mixed surface water, the air, the biosphere, the ocean bulk thus changing the carbon content, m of the surface, the air, the biosphere, and the ocean bulk. The flow rate of anthropogenic carbon from the surface to the bulk of the ocean water by diffusional mass transfer between the secondary currents of equilibrated water and the bulk can be denoted Fbulk according to
Fbulk = dmbulk / dt (1b)
The net sink flow rate to the biosphere can be denoted Fbio according to
Fbio = dmbio / dt (1c)
The two first terms of equation (1) describe the accumulation in the complete backmixed part of the absorber. They are dependent of each other because the chemical composition of the back-mixed layer is in rapid movement towards equilibrium with the air. For the carbon dioxide component, this equilibrium will obey Henry's law according to:
![]()
where Csurf is the concentration of carbon dioxide in the equilibrated surface water, kH is Henry's constant, and Cair is the concentration of carbon dioxide in the air (ppm). According to basic inorganic chemistry, the ratio between the concentration of carbon dioxide (including H2CO3) in the surface water and the total carbon content in the backmixed surface water, msurf, should be constant. We denote this constant by y according to
![]()
The ratio between the atmospheric carbon dioxide concentration and the carbon content of the atmosphere is constant also, z = 1 ppm / 2.123 GtC:
![]()
Equations (2) - (4) imply that, because of dissolution equilibrium, the atmospheric concentration of carbon dioxide and thus the atmospheric carbon content always must change proportionally to the carbon content of the backmixed surface water:
![]()
Equation (5) is fundamentally valid. As the chemistry involved in the parameter, y, and in the Henry's constant, kH, is dependent on the temperature (See "Increase of Atmospheric Carbon dioxide Concentration due to Oceanic Warming" on this website), we must assume that the temperature variations of the absorber are less than 1°C.
The balance equation (1) for the anthropogenic emission rate can now, after elimination of the atmospheric accumulation rate by equation (5), be written according to
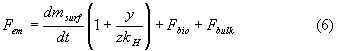
The equation (6) is only valid if the equilibrium in the backmixed part of the absorber is achieved very fastly which means that the backmixing should be complete and the overall gas phase mass transfer coefficient (efficient mixing of the gas phase) must be so high that the diffusion resistance between the gas phase and the surface layer is negligible compared to the diffusion resistances between the atmosphere and the biosphere, and between the surface layer and the ocean bulk.
The net sink flow rate, Fsi, or the flow of carbon that is absorbed from the atmosphere (GtC/a) is defined according to
![]()
Now the change of the carbon content of the surface water can be eliminated from equations (6) and (7) and we obtain the following expression for the net sink flow rate:
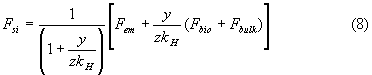
If both Fbio and Fbulk would be constant or proportional to the emission rate, the net sink flow rate, Fsi, would be a linear function of the emission rate, Fem only. In that case the "airborne fraction" would be close to constant.
Flow rate of anthropogenic carbon to the bulk of the ocean water
The flow of anthropogenic carbon from the backmixed surface to the bulk of the ocean water is forced by concentration differences between the equilibrated surface water that secondary currents bring into contact with the bulk. The most simplified way to model this flow rate would be:
![]()
where kL is an overall mass transfer coefficient. If Cbulk is virtually constant (the bulk of the ocean water has still a composition corresponding to the pre-industrial atmospheric carbon dioxide concentration), the flow of anthropogenic carbon to the bulk of the ocean water will be a linear function of the atmospheric carbon dioxide concentration only.
Flow of anthropogenic carbon to the biosphere
The diffusional net absorption rate of anthropogenic carbon to the biosphere is some unknown function of the atmospheric partial pressure of carbon dioxide. As the partial pressure or the carbon dioxide concentration increases, the net sink flow rate to the biosphere (soil, trunks, sinking biomass in the oceans) will increase. Numerous researchers have proved that the growth rate by most plants are dependent of the gaseous carbon dioxide concentration. It the growth rate increases, the accumulation rate will increase also.
It is very common in chemical engineering that an unknown complicated function is simply linearized. This is theoretically justifiable also, according to the Taylor's theory, any continuous function can be approximated by a polynom. Linearization, where only the first order term of the Taylor's serie is taken into accound, always creates a certain robustness if the coefficients are calculated from experimental data by a least-square procedure, but can, of course, also cause errors. On the other hand, a flexible model that contains too many adaptive parameters is dangerous. If we combine equation (9) with our qualitative knowledge of how the biosphere works we can write a linearized relation according to
![]()
where a0 is a constant that is dependent on the product kLCbulk and the behaviour of the biosphere, and a1 is dependent on kLkH and the behaviour of the biosphere also.
Final structure of the net sink flow model
Equations (8) and (10) give:
![]()
or simply
![]()
The chemical engineering model of the absorber can be written as a simple equation where the net sink flow rate is a linear function of both the emission rate and the atmospheric concentration of carbon dioxide.
If we would discover that b2 (or a1 ) is zero or close to zero, we have a situation that corresponds to the "Bern" model used by the IPCC, or the airborne fraction would be almost constant.
If, on the other hand, if b1 has a very small value, we have a mechanism where the net sink flow rate primarily is controlled by the atmospheric concentration or the partial pressure.
Because both b1 and b2 are physically significant, we can already claim that any prediction that implies a constant value of the "airborne fraction" is more or less flawed. Unfortunately, this can be said also about my complete partial pressure controlled model. So far the IPCC modelers have understood the system correctly. But which of these coefficients is dominating in the system ? Is it b1 (IPCC) or b2 (Ahlbeck/Dietze) or both that is dominating ?
Estimation of coefficients by non-linear regression analysis from the CDIAC-database
Now we recall the first equation (1) and combine it with equation (10):
![]()
Because Cair= z mair (equation 4), we can write for the increase rate of the atmopsheric carbon dioxide concentration:
![]()
The CDIAC data are given as the yearly emissions and the atmospheric carbon dioxide concentration. If we introduce the subscript, i = 1 for the year 1960 and i = 38 for the year 1997, we can use equation (14) for calculation of the carbon dioxide concentration for any "next year", i + 1, by using only the anthropogenic emissions "one year", i. We must, of course, use a start value for the year 1960. As the start value we can use the measured value. The atmospheric carbon dioxide concentration according to the model is denoted Cmod.
![]()
where i = 1,2,3, ..... 38 and Cmod,1 = Cair,1 = Cair (1960).
The values of b0 , b1 , and b2 can now be calculated by minimizing the residual sum of squares by means of a numerical search. This means that we try to find the values of the coefficients that explain the measured values at Mauna Loa in the best possible way.
![]()
Results of the non-linear regression analysis
The non-linear regression analysis using a SIMPLEX search algorithm according to Himmelblau (1972) gave the following results:
b0
= - 11.098 GtC/a
b1 = 0.0455 (dim.less)
b2 = 0.03846 (GtC/a/ppm)
The difference between the measured and the modelled carbon dioxide concentration values were small, the residual standard deviation was only 0.57 ppm. Because the deforestation was not taken into account, it means that if we this year emit 6.5 GtC from fossil fuels and cement production, the sink flow at today's atmospheric concentration of 365 ppm would be according to the model:
sink = -11.098 + 0.0455*6.5 + 0.03846*365
= 3.236 GtC
acc. in the atmosphere: 6.5 - 3.236 = 3.264 GtC ( = 1.54 ppm)
The partial accumulation in the upper "backmixed layer" that obeys the "constant airborne fraction rule" is:
0.0455*6.5 = 0.2958 GtC or only 9% of the total net sink
The rest, 3.236 - 0.2958 = 2.94 GtC or as much as 91% of the total net sink is forced by the partial pressure and absorbed to the biosphere and the ocean bulk.
The result indicates that of today's emission from fossil fuels and cement production, about 50 % stays in the atmosphere, 5 % is absorbed somewhere according to a "constant airborne fraction rule", and 45 % in absorbed according to a "partial pressure controlled mechanism".
Estimation of the model coefficients by linear regression analysis from the CDIAC-database
The problem can, using the same data, be solved in a different way by using a linear regression analysis that gives the possibility to test the statistical significance of the two coefficients. The problem must, however, mathematically be formulated in a little different way for the linear analysis.
The model coefficients, b1 and b2 are now calculated by minimizing the residual sum of squares between a vector containing the dependent variable, Fsi , calculated by the model (equation (12), one number for every year for 1960-1997 using global numbers for the emissions and atmospheric concentration of carbon dioxide, and a corresponding vector, Fsink,i , containing observed values for the dependent variable, Fsink,i, calculated directly from the same CDIAC-data according to:
Fsink,i = Fem,i - dmi = Fem,i - (1/z) (Cair, i+1 - Cair, i ) (17)
where i = 1 for the year 1960 and i = 38 for the year 1997. Calculating in this way, we define the sink for each year as the mass of one years emissions of anthropogenic carbon that is fastly absorbed somewhere and cannot be found in the atmosphere next year.
The differentiation can, of course, be carried out in more complicated ways too, for example by using larger time difference and longer time lag for the atmospheric concentration response combined with moving averages (slower equilibrium with the surface layer and/or thicker surface layer). I have tried almost everything I could find out, but nothing could change the basic finding written in the end of this report. I did not take the net emissions due to deforestation into account. If this contribution has been rougly constant during the period, it will not disturb the structure of the calculation.
In the "Backward Elimination Procedure" we can let the computer decide which of the coefficients b1 or b2 , or both, the regression analysis will accept as important.
The intercorrelation problem
The intercorrelation between the two independent variables Fem and Cair is strong which means that a statistical analysis does not need both independent variables in order to explain the dependent variable. The anthropogenic emissions have increased simultaneously with the increase of atmospheric carbon dioxide. One of the independent variable will therefore most probably be kicked out of the regression. If we have bad luck, the wrong variable is eliminated. This is usually called "nonsense-elimination". Some people have achieved high academic degrees with the help of a nonsense-elimination that gives unexpected and theoretically interesting results.
The intercorrelation problem can be avoided by careful experimental design, the anthropogenic emissions should experimentally be changed independently of the atmospheric concentration of carbon dioxide. Unfortunately, we have not been able to carry out such experiments with our absorber. In the process industry this problem is very common: we are not allowed to perform any planned experiments that can disturb the production process, and still we must try to discover how the process really works using only on-line measured, more or less intercorrelated data vectors from the production process.
But as in this case, small characteristic variations in the measured process parameters can often be enough for the regression analysis to choose the physically correct independent variables for explaining the dependent variable.
The breakdown of the Soviet Union created a useful disturbance in the emission curve that is automatically utilized by the calculation. But most important is the clear linearity of the carbon dioxide curve during recent years which in the regression analysis automatically favours the coefficient b2 because the increase of the emissions has been close to linear too. The only thing that would favour b1 would have been a parabolic shape of the carbon dioxide curve with an increase of the derivative proportional to the emissions.
A fair competition between the two coefficients
A backward elimination regression procedure provides a fair competition between the intercorrelated independent variables with a certain risk of nonsense-elimination. But a nonsense-elimination usually demands that the difference between the initially calculated partial Fischer's values (or partial t - values) for the independent variables is very small.
In this case the difference was remarkable. I got the first regression equation containing both variables where the partial Fischer's values (a measure of the statistical significance of the variables) for both Fem and Cair both were low due to the internal correlation. The initial regression analysis gives:
For Fem (b1): partial Fischer's value = 0.151
Cair (b2): partial Fischer's value = 0.758
The "Backward Elimination Procedure" kicks b1 or the direct dependence of the net sink flow rate on the emission rate or out of the regression and keeps the partial pressure with a safe marigin. This is does not look like a nonsense-elimination. The partial Fischer's value for b2 when the partial pressure remains alone in the regression jumps up to 22 as the atmospheric carbon dioxide concentration remains in the regression as the only factor that explains the experimentally obtained net sink flow rate.
The net sink flow rate from fossil fuels and cement production can thus be estimated with the simple equation:
Fsi = - 15.0623 + 0.0513 * Cair (18)
The contribution from deforestation is, as mentioned before, not taken into account. If it has been roughly constant, it will not change the main finding that the absorption is primarily controlled by the partial pressure. If the deforestation rate has increased, the partial pressure controlled absorption mechanism is even more likely because we have measured a very slow increase of the carbon dioxide concentration during recent years.
This result is, when taking the stochastic nature of the system into account, in very good agreement with my previous results obtained from CDIAD-data for the shorter period 1970-1997 where deforestation was included. These results were calculated in a rather different way through regressional linearization of the original data vectors.
Finding a reliable value for b1 by theoretical calculations
We cannot, of course, state that the "real" value of b1 is physically zero, although eliminated as statistically insignificant from the regression analysis. (The non-linear regression gave a value of 0.0455). Due to the intercorrelation, one of the coefficients has to be eliminated anyway. We must therefore try to discover a reliable value for b1 in some other way. The coefficient has a physical definition according to
b1 = 1/(1+y/zkH)
In order to find this value, we can not use the CDIAC database anymore, we must use for example use the scientifical information provided by the IPCC combined by a computerized simulation of the chemical equilibrium for the ocean surface. When we have found this value, we must correct the value of b2 obtained by the linear regression analysis in order to maintain the carbon balance.
The carbon budget presented by the IPCC (1996), page 79, Table 2.1. shows that the total ocean uptake has been 2.0 GtC/a if the total anthropogenic emissions have been 7.1 GtC/a. If the whole ocean uptake would have been accumulation to the backmixed surface layer, and no transport from the surface to deep water would take place at all. the value of b1 should be 2.0/7.1 = 0.282 which means that y/zkH @ 2.546.
Chemical equilibrium calculations (Westerlund 1990) show that an "equivalent ocean layer" thickness of about 350 m is needed to explain the ocean sink of anthropogenic carbon during recent years when also the contribution from deforestation is taken into account. The directly backmixed layer thickness is, however, according to numerous investigations, between 50 and 200 m dependent on location, wind, and currents. The average thickness is about 100 m. This means that a considerable part of the total ocean net sink of anthropogenic carbon flows away from the surface layer into deeper water. As this diffusional/mixing mechanism is a dynamical process that is controlled by the concentration gradients only (equation 9), it is a clear physical indication for a much lower value of b1 than 0.282 that must be balanced by a high value of b2 in order to maintain the total value of the ocean sink flow.
Westerlund's simulation approximately means that y/zkH @ 2.546 for a layer of 350 m thickness. Because y is, according to the definition (equation (3) proportional to the inverse of the thickness, a completely backmixed layer of only 100 m would imply that the real value of y/zkH @ (350/100)*2.546 = 8.911 and the real value of b1 @ 0.10. But Westerlund did not take the biosphere into account at all, he assumed that the whole sink is oceanic. The real value of b1 should therefore be less than 0.10.
Because of of the "precautionary principle" we could, however, use the higher value, or 0.10 so we are sure not to underestimate the future carbon dioxide concentration.
It is really no wonder that the linear regression analysis did not like the coefficient b1 because the explaining power is small.
Final absorption model, deforestation included
According to the results of the modeling effort and the statistical analysis, I would as a combination of numerous statistical calculations and chemical simulation of the ocean surface, and taking a deforestation rate of 1.6 GtC/a into account, propose the following model:
************************************************
Fsi = - 14.0 + 0.10*Fem
+ 0.05* Cair
************************************************
where all anthropogenic emissions from fossil fuels, cement manifacture and deforestation should be included in Fem.
The influence of the first coefficient is small. This means that my prediction in the report - "The IPCC Carbon Dioxide Predictions are Erroneous" , Figure 6, (on this website) of about 550 ppm for the year 2100 (emission scenario IS92a) is still quite correct. A better value would be a little higher, or about 570 ppm. The IPCC value of about 710 ppm is erroneous.
This model has a clear advantage compared to the IPCC model: It explains the real measured Mauna-Loa curve correctly ! The IPCC model is unable to explain the slow increase of atmospheric carbon dioxide during recent years.
Carbon budget for this year, 1999
If we imagine a balance area for the part of the absorber that contains the has phase and the surface layer, and consider the flows to the biosphere and the ocean bulk as outlets, we can write the following carbon balance:
Inlet
Anthr. emissions including deforestation : 8.10 GtC
Accumulation
Accumulation in the atmosphere (1.43 ppm): 3.04
Equilibrated to the backmixed ocean surface (10 %) 0.81
Outlet
Uptake by the biosphere and the ocean bulk (part.press. controlled) 4.25
Total 8.1 GtC
There are, of course, not the same molecules as emitted that are absorbed. the partial pressure controlled absorption is a continuous process that goes on because of accumulated carbon dioxide in the atmosphere from decades of human activity.
Sink flow rates during different centuries:
in the pre-industrial time (280 ppm):
10 % of emissions
today (365 ppm): 10
% of emissions + 4.25 GtC/a
in the future (2xCO2=560 ppm) 10
% of emissions + 14.0 GtC/a
If we imagine a future emission rate of 17 GtC/a at 560 ppm, there will be a net sink flow rate of 1.7 + 14 = 15.7 GtC/a. The "airborne fraction" would be only 8 % of the total emissions.
The IPCC-model implies a net sink flow rate of only 8.5 GtC/a for this situation !
Conclusion and discussion
The main part of the total net absorption is controlled by the partial pressure, only a small part is direct accumulation into the backmixed surface layer of the ocean and the "upper biosphere". This means that there is a considerable self-damping effect that will moderate the future increase of the atmospheric carbon dioxide concentration
The simplified carbon dioxide model reported by Peter Dietze on this website starts directly from an assumption of partial pressure controlled absorption. The influence of the accumulation in the surface layer and in the biospheric reservoir ir taking into account by introducing a total "accumulation capacity" of atmosphere + 33 %. Although this model gives rougly the same results as my model, I think that my way of modeling the accumulation, starting by Henry's law, is physically a little more reliable.
Some researchers have recently claimed that the capacity of the ocean to absorb carbon dioxide is limited. My calculations of oceanic chemical equilibrium chemistry do not support this statement.
Notation
| a0 | linearized intercept | GtC a-1 |
| a1 | linearized coefficient | GtC a-1 ppm-1 |
| b0 | regression intercept | GtC a-1 |
| b1 | regression coefficient | no dimension |
| b2 | regression coefficient | GtC a-1 ppm-1 |
| C | carbon dioxide concentration | ppm (v) |
| F | carbon dioxide flow rate | GtC a-1 |
| kH | Henry's constant | no dimension |
| kL | mass transfer coefficient | GtC a-1 ppm-1 |
| m | mass of carbon | GtC |
| t | time | a |
| y | ratio | ppm GtC-1 |
Subscripts:
| surf | backmixed surface |
| air | air or atmosphere |
| bio | biosphere |
| em | emission |
| bulk | ocean bulk |
References:
Himmelblau, D.: Process Analysis by Statistical Methods, Wiley & Sons, 1972.
IPCC: "The Science of Climate Change 1995" Cambridge University press, 1996
Jain, A.K., H.S. Khesgi, M.I.Hoffert and D.J. Wuebbles: Distribution of radiocarbon as a test of global carbon cycle models. Glob Biochem. Cycles, 9, 153-166 (1995).
Siegenthaler, U. and F.Joos, 1992: Use of a simple model for studying oceanic tracer distribution and the global carbon cycle. Tellus, 44B, 186-207, 1992.
CDIAC home page, data for carbon emissions from fossil fuels and cement production, measured carbon dioxide concentrations at Mauna Loa., 1999.
Ahlbeck, J.: Statistical programs for linear and non-linear regression analysis in FORTRAN, Abo Akademi University, Internal Report 1995.
Westerlund, T. On Modeling the Atmospheric Carbon Dioxide Change, Report 90-111-A, Abo Akademi University, Laboratory of Process Design, 1990.
![]()
![]()
Return to "Climate Change Guest Papers" page
Return to "Still Waiting For Greenhouse" main page