Little
Warming
with new Global Carbon Cycle Model
by
Peter Dietze
For Review Comments on this paper, click here
![]()
Summary
A new global Carbon Cycle Model with a realistic CO2 e-fold lifetime of 55 years (half-life time: 38 years) reveals that the temperature will increase by ~0.3 degC only if the present global CO2 emission is kept constant until 2100. In IPCC scenarios it is assumed that far more fossil reserves would be burnt than is physically recoverable. Using an eddy diffusion ocean model, the IPCC has grossly underestimated the future oceanic CO2 uptake. Hardly coping with biomass response and taking a double to treble temperature sensitivity, all this has led to an IPCC error factor of up to an order of magnitude. So the projected reduction claims need complete revision. The temperature reduction effect of CO2 and energy taxes planned in Europe will only be ~0.005 degC.
Introduction
One of the main reasons for an assumed future CO2 disaster has been the assumption that this greenhouse gas is accumulating in the atmosphere - leading to the frequently repeated 60% Toronto reduction demand.
It is known that the oceans contain about 50 times more carbon than the atmosphere and may take up to nearly 6 times more CO2 at equilibrium and the photosynthesis of land biota may increase up to 18 Gt C/yr for a concentration doubling (three times the present emission). At present, the oceans are still mostly on a pre-industrial level.
The IPCC's "accumulation" hypothesis needs to be firmly contradicted. Suppose we pour water into a bucket that has a hole. Nobody will state from observation that "about half accumulates in the bucket". This fully depends on the hole, the water level and how much we are pouring.
The problem is easily solved when the global carbon cycle is understood as a dynamic system in the manner of control engineering. The atmosphere has a CO2 decay function with a half-life time of about 38 years as will be shown in the following. If the input function is doubling within the same time span the system response would simply be a linear concentration increase. The increase was misunderstood as a nearly irreversible accumulation - one reason that led to hasty conclusions for negotiating an unnecessary global reduction treaty.
The Lifetime of CO2
A simple waterbox model can be used to explain the atmospheric CO2 lifetime and to find a plausible value (figure 1). The atmosphere is represented by a waterbox, filled up to a level of 350 ppm (in 1988) with 750 Gt carbon (2750 Gt CO2 ). This box is placed in a larger waterbox, representing the ocean.
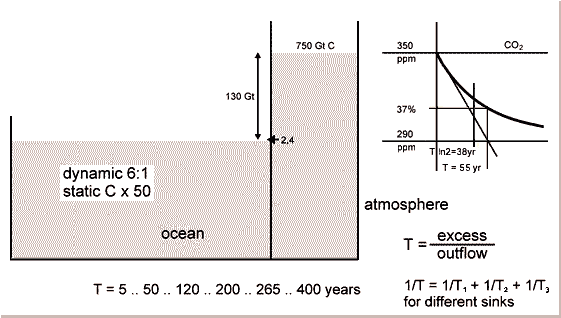
Fig.1: Waterbox Model for the atmospheric CO2 lifetime
The atmosphere box has an outlet, releasing about 2.4 Gt C/yr into the ocean. The level decreases according to an e-function if we postulate the transition flow is roughly proportional to the water level difference or pressure. The lifetime T can be defined as the time lapse until the level goes down to 1/e (37%) against the equilibrium. The value for T can be defined dividing the amount of present excess by the present outflow, yielding 55 years:
(130 Gt + 33%) / (2.4 Gt/yr + 33%) = 55 yr
The 33% stands approximately for extra-atmospheric buffers (fast rotting biomass and surface waters) and extra-oceanic sinks (e.g. trees, polar ice) respectively. For the time interval considered, the small ocean response and the long time for distribution can be neglected.
Multiplication of T by ln 2 yields a half-life time of about 38 years. So any CO2 impulse injected into the atmosphere will take about 38 years to reduce itself to half the original value. Surprisingly this half-life time perfectly matches one remark in a paper published by F. Joos and J. Sarmiento in the German Phys. Blaetter, May 1995 where they say "The oceanic CO2 pickup is slow in comparison to the rate of emission. So for example only half of the CO2 emitted in 1957 is dissolved in the ocean till today". Indeed 1957+38 is 1995...
The Oeschger eddy diffusion ocean model suggestion that the decay will work faster at the beginning and take much longer at the end (363*ln 2 = 251 years), is illogical. Such impulses are continuously injected into the atmosphere and nature treats them all equally, as it cannot distinguish between 'old' and 'new' CO2. Thus this half-life time of 38 years has to be considered as an operational overall value from observed sink flows at present conditions, assuming the reservoirs are big enough and the system behaves in a roughly linear/proportional manner within the operating regime.
If we apply the new carbon model and consider a constant CO2 emission of 7 Gt C/yr (i.e. no reduction) we find that there is not enough carbon to impose a climate problem. This is mainly caused by the atmospheric CO2 lifetime of 55 yr, but also by a smaller temperature sensitivity as well. Another limiting factor is that beyond 2100 we will have to slowly migrate to non-fossil energies (mostly fusion and/or thorium breeders, water power) as conventional fuel reserves become depleted.
Lacking a proper carbon model and ignoring the fact that CO2 lifetime is closely related to sink flows, greenhouse scientists have arbitrarily manipulated this key parameter in the past, stating that no definite value exists or can be defined (see answer of Sir John Houghton on April 2, 1997 at http://members.aol.com/HZingel3/Index.html, section Klima). The IPCC SAR says it is "variable". The question arises as to how the IPCC has calculated future concentrations at all. Often a mean airborne fraction was assumed [1].
In figure 1, some of the lifetime values are shown that have been used. In 1987 the e-fold time was 400 years in Germany (e.g. H. Grassl, E. Maier-Reimer, W. Bach). In 1989 Grassl published 100 years and by 1995 it was 50 to 200 years. The IPCC mentioned 100 and 120 years - but their scenarios mostly used about 360 years for stabilization.
Grassl (WMO) stated, a single lifetime value cannot be defined because of different sinks. This doesn't hold up. Suppose the atmosphere box in figure 1 has three different outlets representing small, medium and large lifetimes. The resulting value is equal to the sum of stored carbon excess, divided by the sum of sink flows. So the value for parallel sinks is
1 /T = 1/T1 + 1/T2 + 1/T3
The 120 years which had been gained by the arithmetic mean from different sinks of the Bern model, are incorrect. The smallest T is leading and a small additional sink flow (large T) does not increase, but decreases the resulting T.
At the low end of the CO2 lifetime we find a value of about 5 years matching the turnover time, published by C. Starr [2] and T. Segalstad [3] - though measurements of the carbon tracer isotope 14C suggest a 1/e lifetime of ~16 years (acc. to GEOSECS surveys, Broecker & Peng, 1993). The turnover time is about an order of magnitude less than if a CO2 mass excess is reduced. For a 5-year lifetime the anthropogenic atmospheric CO2 fraction would be only 4% and the increment stabilized now at 14 ppm. Yet it is unclear how the "calibration" of eddy diffusion ocean models with a radiocarbon lifetime a factor 3.4 less than 55 years has led to missing sinks.
The coupled Waterbox Model
To develop a new global Carbon Cycle Model, the waterbox model was extended (figure 2). Net photosynthesis of land biota amounts to about 60 Gt C/yr, marine photosynthesis is roughly 20 Gt C/yr. The three boxes represent the land biota (700 Gt C), the atmosphere (750 Gt C) and the mixed ocean layer (800 Gt C) which is closely coupled with the atmosphere by precipitation and gas diffusion, exchanging about 100 Gt C/yr with the atmosphere. In high latitudes the icy cold salt water takes up large amounts of CO2 . This is taken into the deep sea and mixing via the conveyor belt into all oceans. The central link is the Antarctic Circumpolar Current.
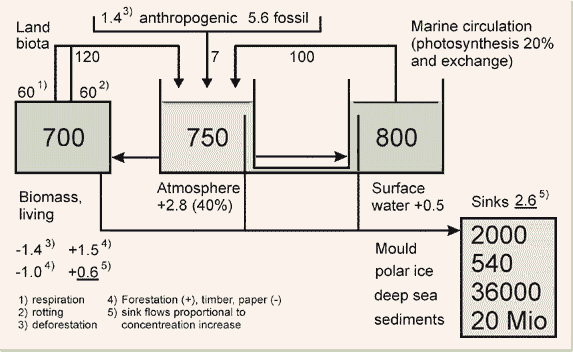
Fig.2: Coupled
Waterbox Model with proportional sink flows
(reservoirs in Gt C, flows in Gt C/yr)
In figure 2 the lower box contains all sinks. A reservoir that takes up CO2 for more than a few centuries is considered as a sink because we need to model no more than 150 years. These sinks are detrius, polar ice, deep sea and sediments including shells and corals. Figure 2 has no missing sinks. These are to be allocated to carbon-fertilized biomass, solubility in the mixed layer, polar water and ice as well as decreasing degassing of upwelling pre-industrial water against the increasing atmospheric concentration. The upwelling water is degassing in tropical latitudes with a time delay of 400 to 1000 years.
The deep sea is still mostly on a preindustrial CO2 level. This means the sink flows will be, in rough approximation, proportional to the atmospheric difference to the CO2 ocean bulk equilibrium [4]. Any greenhouse science statement that the surface water limits the CO2 uptake, thus becoming independent of concentration level (or even reducing with increasing concentration as in IPCC's HILDA model), cannot be verified. So far, a vivid deep water formation has been observed.
Ocean and biota uptake are controlled by the atmospheric CO2 concentration without "knowing" how much CO2 is the human emission. But the HILDA model [5, 6] exactly splits the excess of this emission into the ocean and biota. So in spite of increasing concentration, the ocean and biomass uptake are decreasing in proportion to the emission in IPCC's stabilization scenario S550. This behaviour is absolutely implausible. After the concentration has doubled, the IPCC ocean returns to normal duty taking less than 1.8 Gt/yr. The IPCC biomass returns to about zero net uptake even though photosynthesis probably increases by 30%, i.e. 18 Gt more. The sink flows at 550 ppm are supposed to be about 12 Gt C/yr, that is 6 times more than assumed by the IPCC.
The reason for IPCC's very small stabilization fluxes is the Oeschger/Siegenthaler eddy diffusion ocean model [6, 7, 8]. To support a flux, the diffusion needs a concentration gradient from the mixed layer down to the deep ocean. Because increasing back-pressure builds up, even a constant flux needs a permanently increasing concentration in the air. So to avoid a climate disaster, future emissions have to be reduced considerably with this model - even using a high vertical eddy diffusion coefficient of 7,685 m2/yr - chosen about double the measurement and 3*105 times the original value for diffusion. But in reality the CO2 uptake of the ocean requires an eddy transport and deep water formation model. Here an uptake flux can be maintained rather at a constant difference to the ocean bulk concentration.
The global Carbon Cycle Model with constant emission
Sink flows that are likely to be proportional to increasing concentration, allow a constant global emission at the present rate for another 100 years with minor temperature effect and thus no reduction necessary (figure 3).
The unit decay or Gain Function is G(t) = e-t/T. For the linearized system with an arbitrary emission input E(t), given in Gt C/yr, the concentration in ppm can be computed with the Convolution Integral
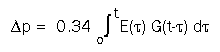
where 0.34 means 100 ppm for every total excess of 294 Gt C (that is, 220 Gt buffered in the atmosphere and 74 Gt in surface water and fast-rotting biomass). Considering the constant emission case we get Delta p = 0.34 ET (1-e-t/T) ppm. Setting E=7 Gt/yr and T=55 yr the concentration increases by 130 ppm for large t.
In figure 3, emission and concentration start with the preindustrial equilibrium to perform a clean cold-start. To match the actual concentration of 350 ppm in 1988 (with a sink flow of 3.2 Gt) the constant emission of 7 Gt C/yr is started in 1950. The concentration increases according to curve (a) as an e-function with a T value of 55 years. The right hand vertical axis shows the proportional sink flow reaching 7 Gt at a maximum concentration of no more than 420 ppm [9].
The temperature scale relative to 1988 shows an equilibrium increment of only ~0.3 K for the next 100 years. This is based on a (logarithmic) sensitivity of 1.4 K for doubling - taking the Hamburg MPIM ocean coupled model value for 100 years after a one-step doubling.
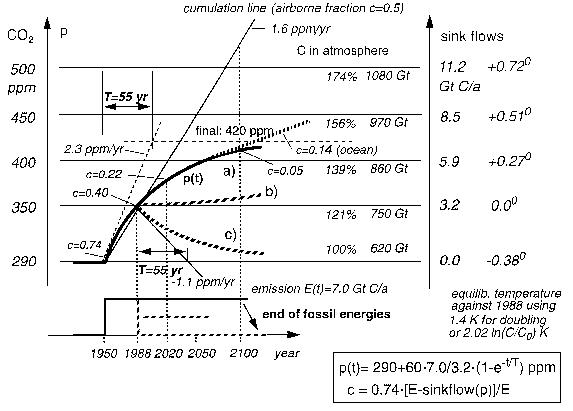
Fig.3: Concentration and equilibrium temperature response of the global Carbon Cycle Model (a) at constant emission, (b) after reduction to 50% in 1988 and (c) after stopping emission
The dashed line at the upper part of curve (a) is a hypothetical ocean equilibrium reaction when taking up nearly six times more CO2 than the atmosphere, caused by the Revelle buffer factor (50/9 = 5.6). But in fact this ocean response can be neglected as it will be mostly delayed by several hundred years. The straight cumulation line shows how an assumed airborne fraction of 50% would yield an increase up to 525 ppm - 75% more than in reality.
Figure 3 presents two further scenarios. Curve (b) shows the response on half the emission beyond 1988. As the emission equals the actual sink flows, concentration and temperature remain quite constant. There is no increment of 2 K as has been claimed in IPCC scenarios and forcing a reduction by 60% until 2050 as documented by Greenpeace [10]. Curve (c) shows a hypothetical stop of emissions in 1988. The concentration decays according to the e-fold lifetime of 55 years, the oceans absorbing most of the CO2 excess within 120 years.
Conclusions
In figure 3 the total temperature increment (caused by CO2) for a constant 7 Gt C/yr emission from pre-industrial times to 2100 is ~0.7 degC. Discussing the effect of the planned carbon and energy tax in Europe, an emission reduction of 4 to 5% has been estimated - this means 0.7% worldwide. The temperature effect will be ~0.7% of 0.7 degC, ie. 0.005 degC. But the EU taxation will be about US$660 billion within 12 years. This seems absurd as the effect is absolutely unnoticible. Moreover the available fossil fuels will be mostly depleted after 120 to 150 years anyway.
Greenhouse scientists have been using a constant airborne fraction of about 50% instead of a realistic CO2 lifetime, arriving at a nearly doubled concentration increment until 2100. Then, taking over twice the real temperature sensitivity and burning much more than the available carbon, the climate impact is boosted by up to a factor of 9. The same holds true in reverse for reduction claims to stay within a given temperature threshold.
The IPCC burns about 2300 Gt C for scenario S750, though the available fossil reserves are 720 Gt conventional or 1.000 Gt including unconventionals as in the IPCC 1995 WG II Energy Primer [11]. The IPCC reference scenario IS92a burns about 1500 Gt C until 2100. Here IPCC's concentration rises up to 680 ppm [12] - far above the 500 ppm that could be reached at maximum if we assume all the conventional fossil fuel reserves are burnt and 40% of the emission remains in the air for a long time.
Considering a total error factor of an order of magnitude, costly activities for `climate stabilization' and high-end model computing become obsolete. Eddy diffusion and HILDA models fail to produce realistic future sink flows. Observations show that solar variability [13] and associated cloud coverage [14] had significant influence and the IPCC may have overestimated anthropogenic forcing up to a factor of 3. Governments, industries and power utilities should carefully check the IPCC climate models before planning costly measures to solve problems that may be irrelevant.
On the IPCC's present shaky base of knowledge it is irresponsible to alert all nations to sign on to an FCCC reduction treaty that may, for example, cost Germany alone DM765 billion and 275.000 primary jobs (acc. to a study by the renowned RWI Institute, Essen, for the projected 25% reduction till 2005).
So IPCC scientists should in future be more circumspect in their claims to avoid the prospect of millions of people suffering from carbon taxes, lack of energy, unemployment and putting the blame back onto them. There is no doubt: -
Reducing IPCC's global warming is much easier than reducing global CO2 emissions.
References
This paper is an abridged excerpt of ESEF Vol. II, 1997 (http://www.esef.org).
[1] Bolin, B.; Döös, B.; Jäger,
J.; Warrik, R.: SCOPE 29. The Greenhouse Effect,
Climatic Change and Ecosystems. John Wiley & Sons 1988
[2] Starr, C.: Atmospheric CO2
Residence Time and the Carbon Cycle. Energy Dec 1993
[3] Segalstad, T.: The Distribution of CO2
between Atmosphere, Hydrosphere and Lithosphere; Minimal Influence from
Anthropogenic CO2 on the Global Greenhouse Effect
in European Science and Environment Forum: "The Global Warming Debate",
London 1996
[4] Dietze, P.: Klimaschutz: Play Bach by Enquête - Falsche
Zeitkonstanten und bis zum Faktor 8 überhöhte Reduktionsforderungen.
Fusion 16 (1995) 3
[5] Enting, I.; Wigley, T.; Heimann, M.: Future Emissions
and Concentrations of Carbon Dioxide: Key Ocean/Atmosphere/Land Analyses.
CSIRO 1994 Technical Paper No. 31
[6] Siegenthaler, U.; Joos, F.: Use of a simple model
for studying oceanic tracer distributions and the global carbon cycle.
Tellus 44 B, 186-207 (1992)
[7] Oeschger, H.; Siegenthaler, U. et al: A box diffusion
model to study the carbon dioxide exchange in nature. Tellus 27,
168-192 (1975)
[8] Siegenthaler, U.; Sarmiento, J.: Atmospheric
carbon dioxide and the ocean. Nature 365, Sept 9, 1993
[9] Dietze, P.: Bei konstanter CO2-Emission
keine Klimakatastrophe. Ein neues globales Kohlenstoffmodell. Europäische
Akademie für Umweltfragen, Leipzig, Nov. 1995 conference papers.
[10] Leggett, J. (edt): Global Warming. The Greenpeace
Report. Oxford Univ. Press NY, 1990
[11] IPCC WG II Vol. Impacts, Adaptions and Mitigation:
Energy Primer, 1995
[12] IPCC Climate Change 1995. WG I Vol. The Science
of Climate Change
[13] Calder, N.: The Manic Sun, 1997
[14] Svensmark, H.; Friis-Christensen, E.: Variation
of Cosmic Ray Flux and Global Cloud Coverage. A Missing Link in Solar-Climate
Relationships. Report 96-6, DMI Copenhagen (http://www.dmi.dk)
Dipl.-Ing. Peter
Dietze D 91094 Langensendelbach, Germany
August 11, 1997
Phone&Fax +49/9133-5371
email 091335371-0001@t-online.de
http://members.aol.com/HZingel3/Index.html
(select Klima & P. Dietze items)
Peter Dietze studied electrical and control engineering. Professional work was in software development for power system control. Special interest in natural sciences, energy and energy politics led to over ten years of intensive private (non-sponsored) work in global warming science with focus on carbon models. Results were published in a dozen of articles and several presentations.
![]()
Return to "Climate Change Guest Papers" page
Return to "Still Waiting For Greenhouse" main page