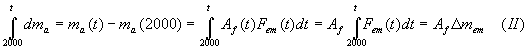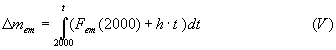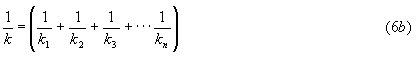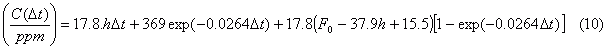|
Carbon
Dioxide Sink 1970-2000 by Docent (env.sci.),
Dr. Tech.
SUMMARY In 1992, the Intergovernmental Panel on Climate Change (IPCC), presented a group of emission scenarios for different greenhouse gases. A "mid-range" emission scenario was called IS92a. However, due to limited fossil fuel reserves, IS92a seems exaggerated when looking 100 years into the future. Numerous new emission scenarios, higher and lower than IS92a, have been created recently. In order to predict future atmospheric carbon dioxide concentrations, emission scenarios may be inserted into computerized global carbon dioxide models. For IS92a, the IPCC claims that the atmospheric concentration would increase from today's value of 369 ppm (ppm=parts per million by volume) to 705 ppm in the year 2100. This is possible only if the rate of atmospheric carbon dioxide increase would very soon begin to increase from today's value of 1.5 ppm/year up to 4 ppm/year. In reality, the increase rate of atmospheric carbon dioxide has, despite the substantial increase of carbon dioxide emissions, remained on a very stable level during the recent 30 years. In fact, the airborne fraction, or the portion of the yearly emissions that stays in the atmosphere, has decreased from 52% in the year 1970 to 39% today. The IPCC model using IS92a implies however a nearly constant future airborne fraction. In this report it is shown that the IPCC carbon dioxide model gives exaggerated future carbon dioxide concentrations for given emissions probably due to underestimation of the sensitivity of the carbon sink flow rate to enhanced atmospheric carbon dioxide concentration. Abstract Data for anthropogenic emissions and atmospheric concentrations for the period 1970-2000 were analyzed by statistical methods. The net sink flow rate of carbon dioxide to the oceans and to the biosphere was found to be strongly dependent on the atmospheric concentration. A pre-industrial value of 275 ppm could be estimated by using statistical data from 1970-2000 only and assuming zero sink flow rate. This pre-industrial value obtained is close to 280 ppm obtained by ice core measurements. A statistical mass transfer model created in this report together with the emission scenario IS92a, gives an atmospheric concentration of 557 ppm for the year 2100, or an increase of 188 ppm for the next hundred years. The IPCC gives 705 ppm for the same emission scenario or an increase by 336 ppm during the next hundred years. The statistical analysis gives a 148 ppm smaller increase than IPCC gives for the same emission scenario. The IPCC predictions seem therefore to be exaggerated to a great extent.
Introduction During the pre-industrial era the atmospheric carbon dioxide concentration has been stable (IPCC 1996). This stability is due to the equilibrium situation when the global carbon dioxide absorption rate of about 220 GtC/a carbon to cold ocean water and growing biomass is balanced by an emission of 220 GtC/a from warm ocean water and decomposing biomass. When the global mean temperature has been high, the equilibrium has changed towards a slightly higher atmospheric carbon dioxide concentration, probably because of decreased solubility of carbon dioxide in the warmer ocean water (Ahlbeck 2000). When carbon dioxide is emitted from fossil fuels, cement production, or deforestation, the increased partial pressure of carbon dioxide in the atmosphere will force an increase of the absorption rate and thus a net sink flow of carbon to the backmixed surface layer of the oceans and to the biosphere. Today, the total anthropogenic carbon emission flow rate is probably about 6.8 GtC/a from fossil fuels and cement production (Marland et al., 2001). A deforestation term must be added to this number in order to get the total emissions. Abt. 3.2 GtC/a (1.5 ppm) of these emissions stay in the atmosphere, and the rest is rapidly absorbed somewhere. IPCC/TAR (2001) gives a net absorption rate to land areas of 1.0 GtC/a (absorbed minus emitted) for the period 1990-1997. For the period 1980-1989 IPCC/TAR (2001) gives a land-use emission (deforestation) in the range 0.5-2.4 GtC/a and a terrestrial sink of 1.8 GtC/a. The oceanic sink has, according to computerized model calculations, increased from 2.0 GtC/a to 2.4 GtC/a in ten years. The uncertainty of the atmospheric accumulation rate is only ± 0.1 GtC/a, but the uncertainty of the emission and absorption rates are as high as about ± 0.5 GtC/a for each number (IPCC/TAR, 2001). As the diffusional mass transfer from the backmixed surface to deep ocean water is slow, the continuous increase of the carbon content of the backmixed surface layer of the ocean will increase the equilibrium partial pressure at the boundary layer of the ocean, thus reducing the enhancing effect of the increased atmospheric concentration on the mass transfer rate from the air to the ocean. On the other hand, the diffusional mass transfer rate from the surface layer to the deep ocean will also increase due to an increase of the concentration gradient. However, if the diffusion to the deep layers is assumed to be a very slow transient process following Fick's second law of diffusion (absorbed carbon dioxide continuously reduces the otherwise increasing gradient), most carbon dioxide modelers produce results that are not very far from a proportional relationship between the anthropogenic emission flow rate and the net absorption flow rate. In other words, the ocean surface-atmosphere-biosphere system would behave as a huge back-mixed batch, and the airborne fraction, or the portion of the emitted carbon dioxide that stays in the atmosphere, would not be very far from constant if these models have a correct structure. The airborne fraction would, according to these models, change only for a significant change in the emission rate, a high emission value giving a high airborne fraction, and a low emission value a low value of the airborne fraction respectively. Analysis of radioactive carbon in the ocean water is also used to calculate the mass transfer coefficients in Fick's second law of diffusion (Siegenthaler and Joos, 1992, Jain et al. 1995). These results are however measured in a situation when the atmospheric carbon dioxide concentration has been much lower than today, which means that the net sink flow rate of carbon dioxide from the atmosphere to the oceans has been low too. The numerical values of these parameters are thus limited in time and calibrated only to reproduce a historical rate of mixing into the ocean. If the bulk of deep ocean water has a carbon dioxide concentration corresponding to an equilibrium pre-industrial atmospheric level of, say 280 ppm, and the atmospheric concentration, C, is higher, a simplified pseudo-steady-state diffusional approach would suggest that the net sink flow rate is some function of the total driving difference C-280 independent of how many and what kind of resistance barriers there are between the atmosphere and the deep water. Models for the biospheric uptake of carbon dioxide describe the carbon dioxide fertilization of plants that is dependent on the atmospheric carbon dioxide concentration (Xiao, et al., 1997). Most models produce a current biospheric sink of only about 1 GtC/yr for 360 ppm atmospheric concentration. When the oceanic models and these models are combined, they can explain only a part of the total carbon dioxide sink. The rest of it is then added to the modeled biospheric sink as a more or less constant term, a residual flux needed to balance the carbon budget (Holian 1998). The question of how sensible the total sink flow rate including the `balancing term' really is for the atmospheric concentration is essential if the models should be used to calculate the future atmospheric concentration for different emission scenarios. A small difference in both the oceanic and the biospheric model structure will give a large difference in the prediction. Most global carbon dioxide models have very low sensitivity for the partial pressure on the oceanic uptake, and a quite large balancing term that is not controlled by the partial pressure in the biospheric model. This means that these models may give results that are quite close to a "constant airborne fraction" mechanism and thus a quite high value for the future atmospheric concentration of carbon dioxide. Holian (1998) obtained great uncertainties in the model prediction of future atmospheric carbon dioxide concentration for a fixed emission scenario due to uncertain numerical values of the model parameters. But he used a fixed model structure. If the model structure were to be changed also, even greater variations in the predictions will be obtained. The "Bern Model" (IPCC 1996, Joos and Bruno) has been widely used as a standard for calculation of the atmospheric concentration from any given scenario. Indirect verification of such models against tracers and against other models are more or less worthless. Instead, the structure of the model should be evaluated against the available statistical data from 1960-2000.
The emission scenario IS92a and the "Bern" model Predicting future emissions of anthropogenic carbon dioxide is impossible. Therefore different scenarios must be used. The most commonly used is the IS92a "mid-range scenario" for total anthropogenic emissions (fossil + deforestation) of the IPCC (1992) report. The increase of anthropogenic emissions is almost constant, 0.114 GtC/a2. In IPCC/TAR (2001) numerous new emission scenarios (SRES) are presented that are based on the decision of the IPCC Bureau at its July 1998 meeting in Germany. During the next hundred years, about 1,400 GtC of anthropogenic carbon will, according to IS92a, be emitted as carbon dioxide. This number can be compared to the fact that most estimations of the known and hypothetical global fossil fuel reserve (coal, gas and oil) give values around 1,300 GtC. There will, according to IS92a, be no future shortage of fossil fuels, and no significant substitution of fossil fuels by other energy sources. The world economy and population numbers will develop roughly in the same way as before. Gerholm (1999) shows that IS92a is hardly a realistic scenario. A probably more realistic scenario that assumes that the carbon intensity will at least continue to decline (or the efficiency of carbon use will increase) at the same rate in the future as it has done for the past 150 years, will end up at an emission of 14 GtC/a instead of 20 GtC/a for the year 2100 (WEC/IIASA 1995). The "Bern" carbon cycle model (IPCC 1996 and IPCC/TAR 2001) gives for emissions according to IS92a:
2050: atmospheric carbon dioxide
concentration
= 503 ppm A further investigation of the presented curve shows that it is a parabola segment. The time-dependent airborne fraction, Af, can be defined according to
where ma(t) is the time-dependent atmospheric carbon content and Fem(t) is the time-dependent anthropogenic carbon emission. We now consider a time period starting from the year 2000 and obtain from Equation (I) the increase of atmospheric carbon after 2000 due to anthropogenic emissions according to:
where Dmem is the total emitted anthropogenic carbon dioxide after the year 2000. Equation (II) is valid only if Af remains on a constant value and can be taken out of the integral. The atmospheric carbon content, ma(t), can be calculated by adding the carbon increase after 2000 to the carbon content for the year 2000 according to:
where Dmem is defined according to:
For IS92a the emission curve is close to linear with a mean slope of h. Thus Equation (IV) can be written according to:
which after integration gives a parabolic expression
The relation between the atmospheric carbon content and the carbon dioxide concentration can be denoted Dma/DC and has a numerical value of 2.123 GtC/ppm. The final equation for calculating the future carbon dioxide concentration from a constant airborne fraction and a linear emission increase can be written according to:
Using the initial values C(2000)=369 ppm, Fem(2000)=8.6 GtC/a, and h=0.114 for IS92a, the future concentrations can be calculated for different values of the airborne fraction. Using Af = 0.5, we obtain for IS92a exactly the IPCC parabola:
Inserting t = 2050 we obtain C(2050) = 504 ppm Inserting t = 2100 we obtain C(2100) = 706 ppm We obtain using Af = 0.5 the same values as the IPCC claims would be a result of the emission scenario IS92a. It is a strange fact that the curve obtained by the computerized "Bern" model can be reproduced from the emission scenario IS92a simply by using a constant value of 0.5 for the airborne fraction. As will be shown later, the airborne fraction has however decreased from 52 % in 1970 to 36 % in 2000 for an emission curve that is very close to IS92a.
Anthropogenic carbon emissions 1970-2000 According to a report from Woods Hole Research Center (2001), the carbon emission from land use change (deforestation) was about 1.6 GtC/a in 1985, and there was an increasing trend of about 0.13 GtC per decade for 1970-1990. These numbers are used when creating an equation for the time-dependent total anthropogenic emissions 1970-2000. The global emissions of carbon dioxide from fossil fuels and cement production has increased from 4.3 GtC/a in the year 1970 to 6.8 GtC/a today (Marland et al., 2001). Regression analysis shows that curve has been statistically linear for the period as no polynomial or exponential parameters were accepted by the regression. We obtain therefore a linear relationship between time and total anthropogenic emissions for 1970-2000:
where Fem is the anthropogenic emission rate including
deforestation (GtC/a), A linear extrapolation into the future gives an emission rate of 18.37 GtC/a for the year 2100 or a smaller number than IS92a (20 GtC/a). The IS92a can thus be considered as a kind of "exaggerated business as usual" (BAU) emission scenario, the emissions increase considerably faster during the next 100 years than during the recent 30 years.
Atmospheric carbon dioxide concentration 1970-2000 The measured atmospheric concentration of carbon dioxide at Mauna Loa (Keeling et al., 2001) can be used as a measure of the globally averaged concentration. In order to level out the stochastic (caused mainly by different ocean temperatures) yearly variations of the increase rate, curve fit by regression analysis was used. The quadratic term, that would have been a sign of a constant airborne fraction for a linear increase of emissions, did not significantly improve the correlation. Despite of that I will later discuss the result of the parabolic curve fit. The exponential curve fit was slightly better than the linear fit, but the statistical significance of bending the curve is still questionable. The exponential equation can be written according to:
where the parameters are: C0 = 324.32 ppm The linear trend was 1.484 ppm/a. These findings are in very good agreement with Hansen et al. (1998) who noticed that the increase rate of the climate forcing due to carbon dioxide has remained on a stable level of 0.025 W/m2/a since 1975. The total climate forcing increase rate for all greenhouse gases has declined from a maximum value of 0.04 W/m2/a in 1975 to roughly 0.03 W/m2/a today because the increase rate of methane and CFC are today both close to zero. A 1 % per year increase rate, that still can be seen in some reports, would correspond to 0.06 W/m2/a or twice the actual increase rate of today. A "business as usual" exponential extrapolation of the carbon dioxide concentration into the future can now be calculated. For the year 2100 we obtain 567 ppm by inserting Dt =130 a into Equation (2). A linear extrapolation from the trend 1970-2000 gives only 517 ppm for the year 2100.
The rate of increase of the atmospheric concentration 1970-2000 from exponential fit By derivation of the exponential Equation (2) we can smooth the yearly increase rates from stochastic noise according to:
Inserting the regression coefficients shows that the rate of increase has risen from 1.39 ppm/a in the year 1970 to 1.59 ppm/a in the year 2000.
The net sink flow rate and the airborne fraction 1970-2000 The net sink flow rate, Fsink can be calculated according to:
The airborne fraction, Af can thus be calculated according to:
Using the regression coefficients we can create the following table for the period 1970-2000:
It is obvious that the airborne fraction has decreased and the decrease is statistically significant for the given emissions and concentrations. The airborne fraction has decreased from 52 % to 39 % during the period. If we consider emissions by fossil fuels and cement production only, the airborne fraction has decreased from 69 % to 49 %. The significant decrease of the airborne fraction 1970-2000 for recent linear increase of emissions is not in agreement with an assumption of a constant airborne fraction for future linear increase of emissions. In order to be sure that the airborne fraction really has decreased, the airborne fraction was also calculated from the parabolic curve fit for the atm. concentration 1970-2000 The second order coefficient was not large enough to cause a constant value of the airborne fraction, the value decreased from 48% to 42%. Many possible physical mechanisms can be suggested for the increase of the sink flow rate and the decrease of the airborne fraction. A logical explanation would be the direct diffusional forcing of the absorption to both oceans and biosphere caused by the increased atmospheric concentration of carbon dioxide. According to Fick's first law of diffusion, the net sink flow would be a linear function of the difference between the actual partial pressure (or concentration, C,) of carbon dioxide in the atmosphere and an equilibrium partial pressure (or concentration, Ceq,) that would give a zero net sink:
where k is a regression coefficient, an overall mass transfer coefficient (in the mass transfer literature usually seen as ka). For a series of n resistances, k is defined as
where k1, k2, k3, .... are considered for example as the mass transfer coefficients air-backmixed surface, backmixed surface-deep water a.s.o. In Equation (6), k is however only an overall statistically calculated mass transfer parameter involving the mass transfer both to the oceans and to the biosphere due to carbon dioxide fertilizing and other possible effects. A statistical analysis for the period 1970-2000 gives the best fit for:
k = 0.0561 GtC/a/ppm Estimated sink flow values by Equation (6) are shown in the last column of Table 1. They are almost identical with to the "measured" values. The obtained regression coefficient 275.5 ppm simply means that the sink flow rate is zero for that atmospheric concentration and that the system is in equilibrium. This result is not very surprising: Data from 1970-2000 indicates that the pre-industrial concentration should about 275.5 ppm, which is, considering the standard deviation of the calculation, not significantly far from the number 280 ppm that has been obtained from ice core analysis.
Prediction for 2000-2100 from given anthropogenic emissions In order to do a prediction for the future, we must assume that the sink flow mechanism according to Equation (6) that has been valid for the recent 30 years will be valid in the future too. We must also define a new time parameter or Dt = (t/a - 2000) If ma is the total carbon content of the atmosphere, a balance equation can be written according to: atmosphere+sink = emitted or atmosphere=emitted-sink (7)
We can then create a differential equation, a "statistical mass transfer model", for calculation of the atmospheric concentration from given emissions according to:
If the emission scenario Fem(Dt) is given numerically, Equation (9) can be solved numerically giving the atmospheric concentration of carbon dioxide for the next century. But if the emission scenario is a linear function of time, there is a simple analytical solution of the equation also. We denote the emissions in the year 2000 by F0 (GtC/a) and the yearly increase (or decrease if negative) of emissions by h (GtC/a2). We also use Dma/DC = 2.123 GtC/ppm and the atmospheric concentration of 369 ppm for the year 2000 as boundary conditions. The solution of the differential equation is:
Calculated results are shown in Table 2:
Table 2. Different estimates for the atmospheric carbon dioxide concentration 2000-2100. If all emissions are stopped today, Equation (10) shows that the atmospheric concentration would start to sink exponentially towards 275.5 ppm, reaching 282 ppm after 100 years. Calculations with the statistical mass transfer model and IS92a gives 557 ppm after 100 years for the emission scenario IS92a when IPCC gives aa concentration of 705 ppm . Interestingly, inserting IS92a in Equation (10) gives about the same result as an exponential extrapolation of the current concentration trend. The parabolic (second order) curve fit for the atmospheric concentrations 1970-2000 gives, extrapolated to 2100, an atmospheric concentration of 610 ppm that still is a low value. Dietze (1998) has presented a simplified physical model based on significant partial-pressure forced diffusion. This model also gives future concentration values much smaller than IPCC.
The WEC/IIASA and IPCC/TAR B2 scenario The WEC/IIASA scenario from 1995 ends up with an anthropogenic emission rate of 14 GtC/a in the year 2100. It is based on the assumption that the efficiency of carbon use will continue to increase as it has done for the last 150 years, a reasonable assumption (h = 0.054) and that the world economy will grow steadily. This scenario is very close to the B2 scenario of IPCC/TAR (2001). Inserting this scenario in Equation (10) gives 487 ppm for the year 2100. The "Bern" model gives for the B2 scenario 600 ppm for the year 2100 (IPCC/TAR, 2001) The difference between the "Bern" model and Equation (10) is 113 ppm for the year 2100. One of them must be wrong, or both.
A chemical ocean equilibrium calculation to 2050 for IS92a emissions without deforestation and biospheric sink Westerlund (1991) has created a chemical equilibrium model for the batch system ocean surface water + atmosphere. As an adaptive parameter for calibration of the model, the "equivalent ocean layer thickness" is used that can be calculated from the amount of water that is needed to balance the carbon budget for the period 1960-2000 so that the known cumulative emissions from fossil fuels and cement production during the period (204.8 GtC according to Marland et al., 2001) will give the known value of the atmospheric carbon dioxide concentration for the year 2000 (369 ppm). The biosphere is not now included, neither as emission from deforestation nor as sink. These flows are now for simplification of the calculation assumed to have been in balance for this period, or the emissions from deforestation are set equal to the biospheric sink. The system is in chemical equilibrium 1960-2000 for an equivalent ocean layer thickness of 290 meters that gives an increase to 369 ppm if 204.8 GtC (emitted from fossil fuels and cement production according to Marland et al.,2001) is added to the gas-liquid batch 1960-2000. The value 290 m is not a real measure of the thickness of the backmixed layer, but a measure of the amount of water (all of the backmixed + a part of the less backmixed) that will give equilibrium for the batch calculation. A calculation of how an even larger amount of carbon dioxide added to the system influences the atmospheric concentration proceeds in the following way: A reference state for the ocean surface, 290 m thick is calculated that is in balance with the atmosphere in 1960. This gives an initial amount of carbon in the gas-liquid batch. Then a new total amount of carbon (the amount 1960 + emissions since 1960) is entered into the air-water batch, and the new equilibrium situation is calculated. This calculation is far from trivial and involves a numerical solution of the pH. IS92a cumulative emissions minus the integrated deforestation contribution gives after integration that 482 GtC should be added to the carbon content of the water-gas batch after 2000, or 687 for the whole period 1960-2050 The ocean calculation gives an atmospheric equilibrium concentration for the year 2050 of 494 ppm. But the "real future concentration for IS92a" must be considerably lower (Equation 10 gives 462 ppm) for two reasons:
It is therefore not suitable to extend the Westerlund further into the future. The obtained concentration 494 ppm should be considered as a maximum limit value for 2050 and IS92a. Equation (10) gives 458 ppm for 2050 and IS92a and one could claim that the Westerlund calculation gives support to that value. The results by the Westerlund model are shown in Table 3. ####### CO2 *** Version 1991-01-21 ** TW ** #######
Mg-balance
Ca-balance
C-balance
H-balance
O-balance
S-balance
Charge-balance
Emission of sulfur
.000 Gton S Table 3. Carbon dioxide equilibrium according to a computer program by Westerlund (1990).
Conclusions The concentration forced sink flow rate has increased during the recent decades. Calculations with both a statistical mass-transfer model and an ocean equilibrium model indicate that the biospheric sink flow is more sensitive for the atmospheric concentration than recently believed which also have been noted by other researchers (Schimel et al., 2000). For the year 2100 and the emission scenario IS92a, the statistical mass transfer model based on known emission- and concentration values for 1970-2000 gives a concentration of 557 ppm or a value 147 ppm smaller than the IPCC-value of 705 ppm obtained with the "Bern" model. IS92a is however hardly possible as it means that nearly all known and hypothetical fossil fuel reserves would be destroyed within only 100 years. References Ahlbeck, J., 2000: The Carbon Dioxide Thermometer. Energy & Environment, Vol. 11, No. 3, pp. 355-358. Dietze, P., 1998: Der Klima-Flop des IPCC. Klima 2000 2, pp 5-6. http://www.wuerzburg.de/mm-physik/klima/cmodel.htm Gerholm, T.R.,: 1999: Energy Use and Climate Models. In: Climate Policy after Kyoto, T.R Gerholm (ed.) Multi-Science Publishing Co Ltd, pp 78-89. (www.multi-science.co.uk) Hansen, J., Sato, M., Glascoe, J., and Ruedy, R., 1998: A common-sense climate index: Is climate changing noticeably? Proc. Natl. Acad. Sci. USA Vol. 95, pp 4113-4120 Holian, G.L., 1998: Uncertainty in Atmospheric CO2 Concentration from a Parametric Uncertainty Analysis of a Global Ocean Carbon Cycle Model, M.Sc. thesis, Massachusetts Institute of Technology, Dep of Earth, Atmopsheric, and Planetary Sciences. IPCC, 1992: Climate Change 1992: The Supplementary Report to the IPCC Scientific Assessment. Cambridge University Press, Cambridge,UK IPCC, 1996: Climate Change 1995: The Science of Climate Change. Cambridge University Press, Cambridge UK IPCC, 2001: WGI Third Assesment Report, Draft. Jain, A.K., H.S.Kheshgi, M.I. Hofferet and D.J.Wuebbles 1995: Distribution of radiocarbon as a test of global carbon cycle models. Glob.Biochem.Cycles, 9, 153-166 Keeling, D., and T.Whorf 2001: Atmospheric CO2 Record from Mauna Loa. Scripps Inst. of Oceanography http://cdiac.esd.ornl.gov Marland, G., T.Boden and R.J. Andres 2001: Global, Regional and National Carbon Dioxide Emissions From Fossil-Fuel Consumption. Univ. of North Dakota, Oak Ridge Nat. Lab. http://cdiac.esd.ornl.gov Siegenthaler, U. and F. Joos, 1992: Use of a simple model for studying oceanic tracer distributions and the global carbon cycle. Tellus, 44B, 186-207. WEC/IIASA 1995: Global Energy Perspectives to 2050 and Beyond. N. Nakicenovic (Study Director). WEC/IIASA Report. Westerlund, T., 1990: On Modeling the Atmospheric Carbon Dioxide Change. Report 90-111-A, Abo Akademi University, Department of Chemical Engineering. (tapio.westerlund@abo.fi) Woods Hole Research
Center, 2001: Understanding the
Global Carbon Cycle. Xiao, X., et al., 1996: Relative Roles of Changes in CO2 and Climate to Equilibrium responses of Net Primary Production and Carbon Storage of the Terrestrial Biosphere, MIT JPSPGC Report No. 8, Cambridge, MA.
Notation Af airborne fraction --
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||