A
LUKEWARM GREENHOUSE -
How `Warm' Will Global Warming Get?
by
John L. Daly
(Based on a presentation and paper, Daly, John L., "Greenhouse: A Dissenting View", to the University of Western Sydney Centenary Conference, November 1992, published in Burgin, Shelley (Ed), "Climate Change: Implications for Natural Resource Conservation", University of Western Sydney 1993, ISBN 1-86341-081-3)
![]()
Introduction
The Greenhouse Effect is a natural phenomenon which allows the Earth to enjoy it's present balmy temperature of 150 C. It results from the recycling of radiant infra-red energy within the atmosphere caused by `greenhouse gases'. By far the most important of these is water vapour. Other natural greenhouse gases include carbon dioxide (CO2), ozone, methane and nitrous oxide, and it is the accumulation of CO2 in the atmosphere which lies at the root of the present controversy about climate change. The pre-industrial level of atmospheric CO2 was 280 parts per million (or 0.028% of the atmosphere), and has risen this century to 360 ppm (0.036%).
Re-cycling of Infra-Red Energy
The effect of this increase in CO2 concentration is to intensify the recycling of infra-red energy within the atmosphere, thus making the surface warmer - but how much warmer? Herein lies the core of the controversy. The present energy `flux' at the surface of the earth is 387 watts per square metre (wm-2), 148 wm-2 of which results directly from the recycling action of the Greenhouse Effect. The other 239 wm-2 is solar insolation, ie. light and heat energy from the sun reaching the surface.
According to Dr Hugh Ellsaesser's IPCC submission, "The direct increase in radiative heating of the lower atmosphere (tropopause level) due to doubling CO2 is 4 wm-2. At the surface it is 0.5 - 1.5 wm-2". Schlesinger & Mitchell (1985), estimated this surface flux at 2 wm-2. Thus, depending on the model, or modeler, the estimates for increased surface flux following a CO2 doubling, varies between +0.5 and +2 wm-2. An above-averaged figure of +1.5 wm-2 will be assumed here for purposes of analysis and comparison.
However, some modelers view the whole troposphere as a single `boundary layer', ie. the entire atmosphere from the surface to about 15 kilometres altitude. At that height, the atmospheric barrier zone known as the `tropopause', separates the turbulent troposphere below from the much quieter stratosphere above. Radiative-convective models calculate the increased radiant energy retention, not only at the surface where we live, but also at the tropopause, where the increased energy retention due to a hypothetical doubling of CO2 is calculated to be, not +1.5 wm-2, but up to +4.5 wm-2.
In some instances, this +4.5 wm-2 tropopause figure has been applied directly to surface conditions, resulting in warmer model temperatures than would be the case if the +1.5 wm-2 surface flux were applied. (Actual temperatures at the tropopause are typically -60 deg. with one-fifth the surface atmospheric pressure).
The increased flux recycling of +1.5 wm-2 at the surface must be considered the more relevant, especially as the oceans can only be warmed by the surface flux, and it is the ability of the oceans to warm (or not warm) which will determine how much global warming we might ultimately get.
And how much warmer? According to the Stefan-Boltzmann equation (E=kT4) which relates energy to temperature (E is energy in wm-2, T is temperature in degrees Kelvin, and `k' is the Boltzmann constant), temperature increases are very small for any given energy increase. Climate modelers claim that `climate sensitivity' (ie. the amount of temperature change for any given energy change) is between 0.7 and 1.1 degC for every 1 wm-2 of energy increase. A `1 to 1' ratio is often cited (eg. Henderson-Sellers, 1989), ie. a +1 deg warming for every +1 wm-2 of increased flux. This assumption is built into the models.
But is this assumed 1 - 1 ratio observed in the real world?
Six separate approaches can be employed to determine the temperature-raising effect of increasing the surface energy flux by +1.5 wm-2, as would result from a doubling of CO2. These can then be compared against similar estimates for global warming that the models give.
1) Compare the existing greenhouse effect with the rise in temperature caused by it:
Without the Greenhouse Efect, the planetary temperature of the earth would be -18 degC assuming (unrealistically) that albedo (the planet's reflectivity) stays constant. The mean global recycled energy caused by greenhouse absorption is 148 wm-2. This can simply be divided by the warming it allegedly causes, namely 33 deg. (the difference between -18 degC and the present surface temperature of +15 degC) Thus 148/33 is nearly 4.5 wm-2 per degree. This means that enhancing the greenhouse effect by +1.5 wm-2 (as might happen with a doubling of CO2) can only give a warming of around +0.33 degC.
(If the models sensitivity ratio of 1 deg per 1 wm-2 were applied, then 148 wm-2 of greenhouse energy added to a hypothetical non-greenhouse global temperature of -18 deg, would give a global temperature today of 130 degC!, a patently ridiculous outcome).
2) By calculation:
Using the Stefan-Boltzmann equation again (E=kT4) , the likely warming resulting from a +1.5 wm-2 energy flux increase can be calculated by increasing `E' in the equation from 387 wm-2 (the present mean flux at earths surface) to 388.5 wm-2 , (the expected flux after a CO2 doubling). This method gives a warming of +0.28 degC.
3) By comparing changes in solar insolation with the resulting changes in temperature:
The Earth does not orbit the sun in a neat circle, but rather in an elongated ellipse, with the sun offset from its centre (see fig. 1). The resulting solar radiation received is not constant throughout the year, but varies by nearly 7% between January and July. This phenomenon is quite unrelated to the seasons. This causes solar insolation at the equator to be about 21 wm-2 greater in January than in July. The temperature changes which result from this are less than 2 degC. (eg. as recorded at Thursday Island, Queensland, on latitude 11 deg. South).
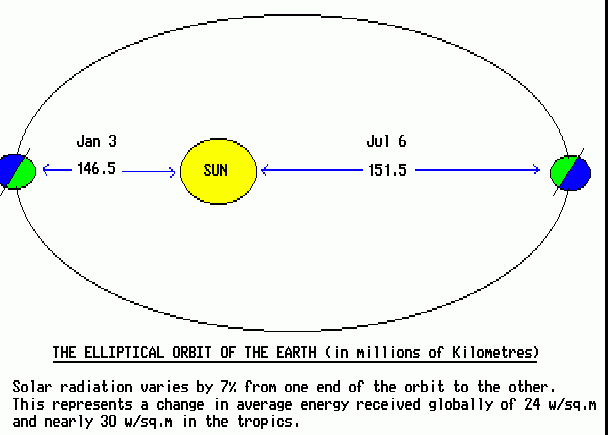
Fig 1: Elliptical Orbit of the Earth
Thus, if it takes 21 wm-2 to change temperature a mere 2 degrees, the warming to be expected from +1.5 wm-2 is only +0.14 degC.
While the 2 degC annual variation at Thursday Island is fairly typical of the tropics generally, the variation reduces to a mere 1 degC. on the Equator itself in spite of a large variation in solar energy through the year. So, we can expect little change at the equator in response to an enhanced Greenhouse Effect.
4) By comparing temperature and energy with latitude:
TEMPERATURES AND ENERGY FORCINGS AT VARIOUS LATITUDES
|
Location |
Latitude |
Net Solar |
Greenhouse |
Total Energy |
Mean Temp. |
|
Singapore |
01 N. |
305 |
210 |
515 |
28 |
|
Thursday I. |
11 S. |
300 |
187 |
487 |
27 |
|
Moreton I. |
27 S. |
280 |
172 |
452 |
21 |
|
Maatsuyker I. |
44 S. |
217 |
152 |
369 |
11.5 |
|
Macquarie I. |
55 S. |
163 |
130 |
293 |
5 |
|
Mawson Stn. |
68 S. |
88 |
80 |
168 |
-11.5 |
(* Based on data from Ramanathan & Collins, "Nature" May 1991, vol.351 and on calculations of average solar radiation, less 30% albedo, at various latitudes; and on station data from the Australian Bureau of Meteorology).
Average absorbed solar and greenhouse radiation over the equator is 515 wm-2, resulting in a measured mean equatorial temperature of around 28 deg. However, At mid-latitudes, such as Maatsuyker Island, Tasmania, at latitude 44S, the total forcing reduces to 369 wm-2 , giving a temperature of 11.5 deg.
| The temperature gradient between Maatsuyker and the Equator is - |
28 - 11.5 = 16.5 degC |
| while the energy gradient is - | 515 - 369 = 146 wm-2 |
Thus, 146 wm-2 is required to change the mean temperature by 16 deg., or 0.11 degC per wm-2 . This same gradient of 0.11 deg per wm-2 exists between the equator and Mawson Station in the Antarctic. On this basis, an increase of +1.5 wm-2 , due to a doubling of CO2, can be expected to raise temperature by a mere +0.16 degC.
5) Perform radiation experiments in the field:
Low level dust in the air traps and re-radiates infra-red energy just like greenhouse gases. Field experiments with dust clouds by Prof Sherwood Idso in the Arizona Desert and on the Pacific coast of the USA, measured and compared temperature changes against the infra-red energy changes causing them. The same exercise was done with weather fronts, where a surge of humidity (ie. water vapour - a greenhouse gas) also causes enhanced back-radiation.
Idso found that +1 wm-2 over land raises temperature +0.18 deg, while +1 wm-2 in a marine environment raises temperature only half as much, ie. +0.09 deg. With 71% of the Earth covered by water, this suggests that climate sensitivity is only 0.113 deg per wm-2 , a result entirely consistent with the latitude comparisons in method [4].
This further suggests that a doubling of CO2 will raise global temperature by only +0.17 degC.
6) Observe and measure the effect of major radiative disturbances in the atmosphere:
The most common events of this type are explosive volcanic eruptions. Recently, we have had the eruption of the Phillipine volcano Mount Pinatubo in June 1991, the most powerful eruption this century. It has been possible to observe the radiative disturbance caused by Pinatubo, using remote sensing from satellites.
The results of these observations was that the blocking and scattering of solar radiation by the stratospheric aerosols temporarily reduced solar radiation to the earth's surface by -4.7 wm-2 .
The Earth cooled, according to CRU, by about -0.5 degC during 1992. The Goddard Institute in New York estimated the cooling at -0.6 degC., while the satellite estimate was about -0.7 degC. So, if we take the average of these three estimates for the 1992 cooling (ie. -0.6 degC.) divided by the change in energy :-
0.6/4.7 = 0.128 degC per wm-2
This gives a very similar sensitivity result to Idso's 0.113 deg per wm-2 in Method [5]. Applied to the +1.5 wm-2 scenario of doubled CO2, this suggests that global temperature will rise by only +0.16 degC.
Conclusion
Remarkably, these six very different methods, all arrive at a very similar result, namely that -
"Global Warming" will be measured in tenths of a degree, not whole degrees.
The average warming predicted by the six methods for a doubling of CO2, is only +0.2 degC.
(During the 1970's, warming predictions were typically around +0.5 degC if CO2 was doubled. The more recent predictions of +1.5 to +4 deg are entirely the product of computer modeling, with no solid basis in actual observations at all).
All this strongly suggests that the models' estimate of 1 deg per wm-2 is quite wrong, and that the true figure is closer to 0.1 deg per wm-2 , ie. only a tenth as much. Note also that five of the above methods include all possible positive and negative feedbacks arising from radiative forcing.
|
Technical Note: "Feedbacks"
are secondary climatic effects such as changes |
Method [2] has no feedbacks, yet gives a higher estimate (+0.28 deg.C) than the overall average. This suggests that the net total of all feedbacks in the real world is actually negative, not positive, contrary to what is generally assumed in the models. This explains why the calculated global warming shown in Method [2] is larger than the average of the other five methods (+0.19 deg.C). It also explains why the Earth's climate has never over-heated or over-cooled during the whole of geological time on Earth.
It is apparent therefore that the model's climate sensitivity estimate of 1 degree per 1 wm-2 is unsupportable, and that a more accurate sensitivity figure is closer to 0.1 degree per 1 wm-2 , ie. only a tenth as much. In short -
The models have built a Greenhouse mountain upon a CO2 molehill.
![]()
Return to "Still Waiting For Greenhouse"